在第2章，本书介绍了完全平稳STAR模型的线性性检验，以如下LSTAR（1）为例做简单回顾^[4]：

式中，φ11＜1，（φ11+θ11）＜1，φ11（φ11+θ11）＜1，以保证STAR模型的完全平稳性。根据Teräsvirta（1994），在式（3.17）基础上进行线性性检验，原假设为H0：γ=0，为克服在原假设下参数的不可识别，对平滑转移函数进行关于γ=0的三阶泰勒展开，结果为

在原假设下，r（γ）=0，将式（3.18）代入式（3.17），得

在原假设H0：γ=0下，式（3.19）的常数项为0，并且yt-1对应的参数仅为φ11，以及渐近等价于εt，此时原假设等价于：H0：β2=β3=β4=0，因此约束模型可表示为(www.daowen.com)

可以构造LM统计量或者Wald统计量检验模型的线性性，定义Wald统计量W0，如果是STAR（p）模型，定义相应的Wald统计量为，则有

式中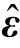，表示非约束模型的残差向量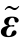，表示约束模型的残差向量。在原假设下，如果约束模型是平稳的，即φ11＜1，那么W0服从自由度为3的χ2分布；但如果约束模型是随机游走过程，即φ11=1，W0的极限分布并不是常规的χ2分布。

目前，已经有文献开始对此问题进行讨论，如Kilic（2004），Harvey和Leybourne（2007），Harvey等（2008）。但他们的研究均是在一阶泰勒展开的基础上进行的，并且仅讨论了原假设是随机游走的情况。对此，本书将在局部非平稳STAR框架下，更为深入地讨论线性性检验问题：一方面，将已有文献的研究框架拓展到在三阶泰勒展开下进行，使其更具有广泛适用性；另一方面，本书不仅讨论了局部随机游走STAR过程，还讨论了局部随机趋势STAR过程以及含有确定性趋势的STAR模型的线性性检验。