类似于线性ARMA模型的建模过程,当估计出模型的参数后,建模者需要对所估计的STAR模型进行诊断和评价,这个过程主要是针对残差的评价及模型误设检验来完成的,Eitrheim和Teräsvirta(1996)及Teräsvirta等(2010)对此进行了详细的阐述,本节简要介绍STAR模型的评价。STAR模型的评价主要包括三个部分——误差项无自相关检验、无非线性剩余检验以及不变参数检验,这三个检验都是通过构建LM类或者F类统计量完成的。
1.误差项无自相关检验
采用与Teräsvirta等(2010)相同的表述方式,假设条件均值m( zt;θ)在样本空间内关于参数至少二次连续可微,并且有
式中,α=(α1,α2,…,αq)′,vt=(ut-1,ut-2,…,ut-q)′,xt=(1,y1,y2,…,yp)′,θ=(φ′,ψ′,γ,c)′,误差项无自相关的原假设为α1=α2=…=αq=0,为构建LM检验的辅助回归式,需要求出如下偏导:
对于LM检验,可以通过TR2形式来完成,因此STAR模型误差项无自相关检验的步骤如下:
(1)估计式(2.38)在原假设下的约束模型,提取残差ut˜,并计算残差平方和![]()
(2)计算wt及vt在原假设下的估计值 和
和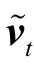 ,计算
,计算 对
对 和
和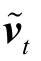 进行回归的残差平方和SSR1。
进行回归的残差平方和SSR1。
(3)计算F类统计量FLM,在完全平稳条件下,FLM~F(q,T-n-q)。
在原假设下,如果假定误差项服从独立的正态分布,则上述无自相关检验即误差项的独立性检验,在应用中,可以采用Brock-Dechert-Scheinkman独立性检验(以下简称BDS检验)来考察模型的残差是否近似为独立同分布过程。
2.无非线性剩余检验
在实际应用中,当一个两区制的STAR模型并不能充分刻画数据的动态波动特性时,其残差部分具有非线性剩余,此时,建模者需要增加STAR模型区制的个数,重新估计模型的参数,直至残差近似为独立同分布过程。因此,无非线性剩余检验实际上也是一种多区制STAR模型的检验。Eitrheim和Teräsvirta(1996)及van Dijk和Franses(1999)分别提出了用于检验非线性剩余的LM类检验统计量。
Eitrheim和Teräsvirta(1996)采用了在两区制LSTAR模型的基础上增加额外的平滑转移函数,构建如下的检验式:
式中,G(s2t;γ2,c2)表示另外一个平滑转移函数,无非线性剩余的原假设为H0:γ2=0,为避免参数在原假设下的不可识别,Eitrheim和Teräsvirta同样采用三阶泰勒展开形式:
式中,xt的含义与式(2.38)相同,当s2t是 其中的一个元素时,
其中的一个元素时, =(y1,y2,…,yp),否则,
=(y1,y2,…,yp),否则, 与xt相同;原假设变为H0:β1=β2=β3=0,在此原假设下
与xt相同;原假设变为H0:β1=β2=β3=0,在此原假设下![]() 渐近等价于εt。在式(2.43)基础上,可以很容易地构建LM类或F类统计量进行无非线性剩余检验,其检验步骤类似于上述线性检验,此处不再赘述。
渐近等价于εt。在式(2.43)基础上,可以很容易地构建LM类或F类统计量进行无非线性剩余检验,其检验步骤类似于上述线性检验,此处不再赘述。
van Dijk和Franses(1999)提出了一种多区制STAR模型(multiple regimes STAR,MRSTAR):(https://www.daowen.com)
式中,F1(s1t;γ1,c1)与F2(s2t;γ2,c2)表示两个不同的logistic平滑转移函数,式(2.44)的模型最多可以形成4个不同的极端区制。类似地,这种“细胞分裂”形式的模型可以扩展到有k个平滑转移函数的情况,会形成2k个极端区制。
van Dijk和Franses(1999)建议采用“从特殊到一般”的模型设定方式检验MRSTAR模型的适用性,即先建立一个两区制的LSTAR模型,然后以式(2.44)作为备择假设,检验所估计的两区制LSTAR模型是否充分,为此,将式(2.44)重新整理成下式:
不失一般性,假定F1(s1t;γ1,c1)为两区制LSTAR模型的平滑转移函数,检验MRSTAR模型是否适用,等价于检验原假设γ2=0是否成立,由于在此原假设下,参数不可识别,所以再次使用三阶泰勒展开将式(2.45)重新写成
此时,原假设变为H0:=0,i=1,2,…,6,在此基础上,可构建LM类或F类统计量进行检验,在应用中,通常采用辅助回归式构建TR2形式的统计量来完成,为此,首先求出如下偏导:
在中小样本下,F类统计量更为有效,其计算步骤如下:
(1)估计式(2.46)在原假设下的约束模型,提取残差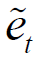 ,并计算残差平方和
,并计算残差平方和![]()
(2)以残差 为因变量,对自变量
为因变量,对自变量![]() =1,2,3进行回归,计算残差平方和SSR1。
=1,2,3进行回归,计算残差平方和SSR1。
(3)计算F类统计量FMR,在完全平稳条件下,FMR~F [6p,T-(2p+2)-6p]。
如果式(2.49)拒绝两区制的原假设,可以采用NLS或MLE方法估计四区制的MRSTAR模型,然后对估计结果重新进行无非线性剩余检验,直至所估计模型的残差近似为独立同分布过程,无非线性剩余检验结束。
以上的分析也表明,Eitrheim和Teräsvirta(1996)的无非线性剩余检验实际上是van Dijk和Franses(1999)MRSTAR模型检验的一个特例,为增加模型设定的稳健性,在实际应用中,可以同时采用两种方法对所估计的模型进行诊断。
3.不变参数检验
以上所提到的STAR模型都假定其参数是不变的,但如果模型误设或者真实的数据生成过程中确实存在变参数情况,那么所估计的STAR模型表现出具有时变参数特性。Eitrheim和Teräsvirta(1996)提出了用于检验不变参数的方法,将上述式(2.36)的两区制STAR模型改写为
式中,t=t/T,εt~iidN(0,σ2),式(2.51)与式(2.52)定义了两个时变参数向量,其平滑转移函数分别为Hθ(t;γθ,cθ)与Hψ(t;γψ,cψ),平滑转移变量均为t,式(2.50)实际上是Lundbergh等(2003)提出的时变STAR模型(time-varying STAR)。不变参数检验的原假设为H0:γθ=γψ=0,由于存在参数的不可识别问题,所以对式(2.51)及式(2.52)进行三阶泰勒展开,经过参数重新整理,式(2.50)变为
因此,新的原假设为![]() βj=0,j=1,2,…,6,在此原假设及式(2.53)的检验回归式下,可构建LM类或者F类统计量进行不变参数检验,F类统计量的分子自由度为6(p+1),分母自由度为T-7(p+1)。同样,可以采用TR2形式来构建F类统计量,其计算步骤类似于上述线性性检验过程,详细计算过程可参见Eitrheim和Teräsvirta(1996)、Lundbergh等(2003)及Teräsvirta等(2010),本书此处不再赘述。
βj=0,j=1,2,…,6,在此原假设及式(2.53)的检验回归式下,可构建LM类或者F类统计量进行不变参数检验,F类统计量的分子自由度为6(p+1),分母自由度为T-7(p+1)。同样,可以采用TR2形式来构建F类统计量,其计算步骤类似于上述线性性检验过程,详细计算过程可参见Eitrheim和Teräsvirta(1996)、Lundbergh等(2003)及Teräsvirta等(2010),本书此处不再赘述。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






