STAR模型的设定包括线性性检验、平滑转移变量的选择及STAR模型类型的确定三部分。如果线性性原假设没有被拒绝，则建模者考虑建立线性的ARMA模型或ARMA-GARCH模型；如果线性性原假设被拒绝，则在此基础上确定STAR模型的类型及平滑转移变量，建立STAR模型。下面简要介绍STAR模型的设定策略。

1.线性性检验

在计量经济学中，有一些传统的经典方法可用于非线性特征的识别与检验，如McLeod-Li检验、RESET检验以及其他一些基于残差的合成检验（portmanteau tests）等，但这些检验方法都没有特定的备择假设形式，即使拒绝原假设，也只能说明数据存在非线性特征，但其具体的模型设定形式却无法从这些检验中获悉。而拉格朗日乘数检验（以下简称“LM检验”）方法，因其能够检验特定的非线性类型，所以在理论与应用研究中得到了更多的关注。下面简要介绍STAR模型中线性性的LM检验原理。

考虑如下两区制的STAR模型：

线性性检验的原假设为H0：θ2i=0，i=0，1，…，p 或者H0：γ=0，但在这两个原假设下，都存在参数不可识别问题，因此无法获得检验统计量的极限分布。为克服这种参数不可识别问题，Luukkonen等（1988）及Teräsvirta（1994）在LSTAR平滑转移函数的基础上，将式（2.30）中的平滑转移函数进行关于γ=0的三阶泰勒展开，即

则式（2.30）可重新写成

式中，xt=（1，y1，y2，…，yp）′，=（β00，β01，β02，…，β0p），=（β10，β11，β12，…，β1p），=（β20，β21，β22，…，β2p），=（β30，β31，β32，…，β3p），此时，原假设H0：γ=0等价于原假设：β1=β2=β3=0，在原假设下，渐近等价于εt。可构建LM统计量对进行检验，具体步骤如下：

（1）估计式（2.32）在原假设下的约束模型，即ty对xt进行回归，计算约束模型的残差平方和

（2）估计式（2.32）的辅助回归式，即非约束模型，计算非约束模型的残差平方和

（3）令原假设下的LM类统计量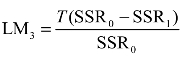，在完全平稳的条件下，LM3～χ2[3（p+1）]；Teräsvirta（1994）建议在小样本下，采用F类统计量，线性性检验功效更高，F类检验统计量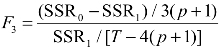～F [3（p+1），T-4（p +1）]。

（4）如果平滑转移变量为yt-d，d＜p，为避免检验回归式中出现完全共线性情况，在原假设中应剔除掉βi0=0，i =1，2，3，因此，LM类检验统计量的自由度为3p，F类检验统计量的分子自由度为3p，分母自由度为T-4p-1。(www.daowen.com)

2.选择转移变量与平滑转移函数类型

为确定平滑转移变量，Teräsvirta（1994）认为建模者可以预先确定一个平滑转移变量的备选集合，我们将其定义为S={s1t，s2t，…，skt}，将集合S中的每一个元素依次作为平滑转移变量，按照上述步骤（1）～步骤（4）进行线性性检验，如果在几个备选平滑转移变量下，线性性检验都拒绝原假设，则选择检验统计量所对应的p值最小的作为平滑转移变量，Teräsvirta（1994）的模拟结果显示，此种选择程序具有较高的检验功效。在实际应用中，集合S中的元素通常为因变量的滞后变量或者差分滞后变量，或是根据特定经济理论选择集合S中的备选元素。

van Dijk等（2002）指出，尽管LM3或者F3是在LSTAR模型基础上构建的，但其同样适用于ESTAR模型，因为ESTAR模型关于γ=0的一阶泰勒近似嵌套于式（2.32），这也表明，在STAR的模型设定阶段，可以先确定平滑转移变量，然后确定平滑转移函数的类型。为确定STAR模型的具体类型，Teräsvirta（1994）在辅助检验回归式（2.32）的基础上提出了三个序贯假设检验：

式（2.33）所表示的三个序贯假设检验都可以通过构造LM类统计量来完成，Teräsvirta（1994）建议：若H02检验统计量所对应的p值最小，应建立ESTAR模型；若H03或H01检验统计量所对应的p值最小，则建立LSTAR模型。

但Escribano和Jordá（1999）指出，采用式（2.32）及上述序贯检验程序确定STAR模型的类型，其检验结果更倾向于选择LSTAR，因为式（2.32）中有两个参数向量含有LSTAR的信息，而仅有一个参数向量含有ESTAR的信息。对此，他们提出将式（2.32）扩展为下式：

在式（2.34）的基础上，他们提出了用于选择STAR模型类型的检验程序：

如果检验统计量所对应的p值更小，则应建立ESTAR模型；如果检验统计量所对应的p值更小，则应建立LSTAR模型。

Escribano和Jordá（1999）的模拟结果表明，对于数据主要集中在转移函数某一区制上的ESTAR模型，Escribano-Jordá检验程序比Teräsvirta检验程序更有效；而van Dijk等（2002）则认为，如果ESTAR模型的数据大部分集中在转移函数的某一侧，那么ESTAR模型可以很好地由LSTAR模型来近似，因此，数据是由ESTAR模型还是由LSTAR模型来刻画显得不再重要，并且他们指出，在实际应用中，“没有哪一个检验程序比另一个更好”。

Teräsvirta等（2010）指出，Escribano-Jordá检验程序的缺陷在于检验回归式中出现了4次多项式，这增加了待估计参数的个数，因而减少了自由度。同时，现代计算技术的发展也使区分LSTAR模型与ESTAR模型的检验程序显得不那么重要了，因为建模者完全可以既估计LSTAR模型也估计ESTAR模型，而在模型的评价阶段确定最终模型。