关于STAR模型总体矩的特性，目前尚未有文献做过讨论，本节通过分析样本矩的统计特性对总体矩进行推断，试图以此获悉更多关于STAR模型的统计性质。

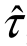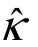Hamilton（1994）总结了协方差平稳过程的样本均值及样本二阶矩的极限分布，在具有序列相关的情形下，样本均值及样本方差仍然依概率收敛于总体均值及总体方差。Kendall和Stuart（1969）讨论了独立正态分布序列的样本偏度估计量与样本峰度估计量的极限分布，即其中，，分别表示偏度估计量与峰度估计量。Bai和Ng（2005）讨论了弱相关序列的样本偏度与样本峰度，并且序列可以是非线性的，令μr，τ，κ分别表示总体r阶矩、总体偏度及总体峰度，则有

上述这些研究表明，对于非线性序列而言，样本均值、样本方差、样本偏度及样本峰度仍然是总体均值、总体方差、总体偏度及总体峰度的一致估计量。因此，可以通过分析STAR模型样本矩的性质获悉更多关于总体矩的性质。下面我们通过随机模拟方法分析STAR模型样本矩的统计特性。考虑如下LSTAR（1）模型^[5]：(www.daowen.com)

式中，自回归系数a={0.1，0.2，…，0.9}^[6]，b={0.1，0.2，…，0.9}，满足STAR模型平稳遍历的充分条件；样本容量T={100，500，1 000，2 000，5 000，10 000，20 000}；门限值c={-3.0，-2.9，…，2.9，3.0}共61个数；平滑转移速度系数γ={1，2，…，30}共30个数。我们设定一个基准的STAR模型：a=0.2，b=0.4，c=0，γ=5，T=100。当分析某个参数变化对样本矩的影响时，只改变这个参数值，而其他参数值保持在基准模型不变，如分析不同门限值对样本均值的影响，我们只改变数据生成过程中的c值，而其他参数均与基准模型相同。在样本容量小于10 000时，Monte Carlo模拟次数均为10 000次；当样本容量超过20 000时，Monte Carlo模拟次数与样本容量相同。

下面分别分析不同自回归系数、门限值、平滑转移速度对样本均值分布、样本方差分布、样本偏度分布及样本峰度分布的影响。其中，样本均值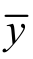、样本方差s2、样本偏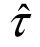态、样本峰态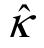分别表示为