1.模型参数反演方法

模型参数的反演算法采用Marquardt-Levenberg优化算法，该算法被验证能够有效地对非线性拟合问题进行反演，并为程序所利用（Kool等，1987；Simunek等，1998）。模型用来反演的目标函数为（Simunek等，1998）：

式中：mq是不同测量数对的数目；nqj是特定测量数对的数目；代表在时刻t时第j个测量在位置x处的测量值；qj（x，ti，b）代表相应的模型预测值；vj和wi，j为对应的权重。

2.模型参数反演结果

由于模型中的水力和溶质参数较多，且各个参数间具有一定的相关性，因此在参数反演中找到唯一解并不总是可能的，因此，为了尽可能减少反演参数的数量，将土壤层按照犁底板结层分为上下两层的土壤参数进行拟合。参数反演所采用的数据为CL10从2007年10月1日至12月24日的地下水和土壤含水量的数据。反演结果如图6-5～图6-8所示。

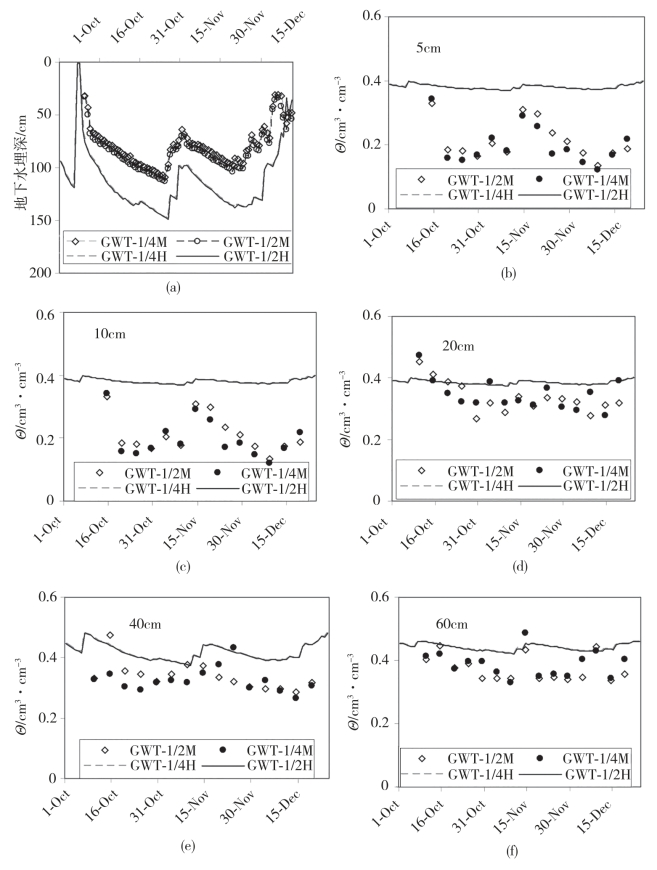
图6-4　BEST试验参数的Hydrus模拟结果

图6-5　模拟（线）与实测（点）地下水埋深对比(www.daowen.com)

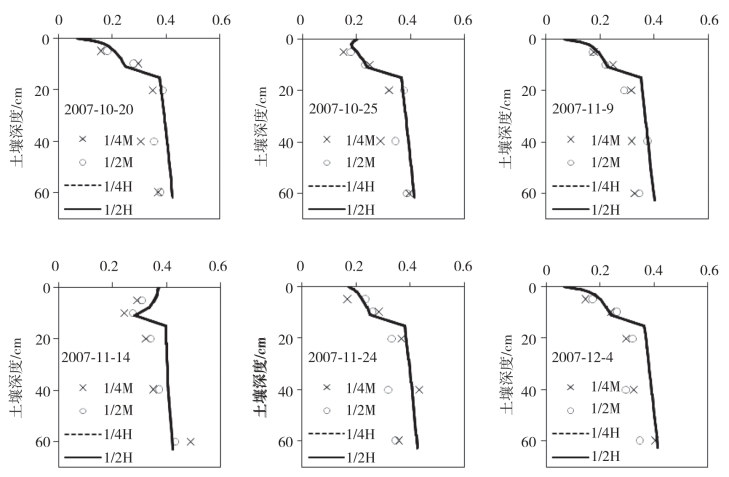
图6-6　模拟（线）与实测（点）剖面土壤含水量对比

图6-7　模拟（线）与实测（点）土壤含水量时间序列对比

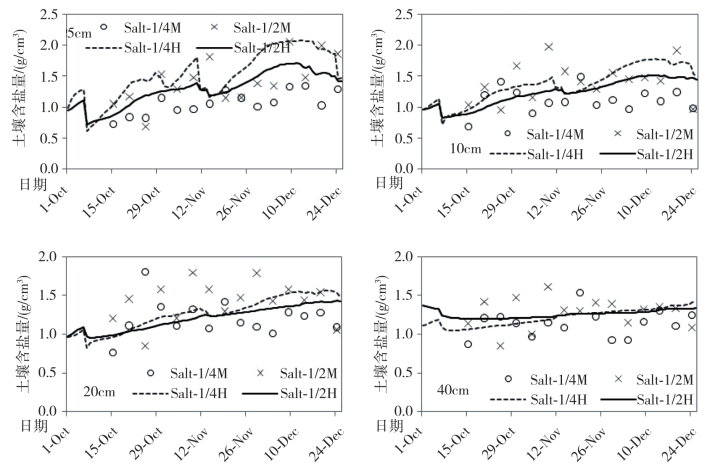
图6-8　模拟（线）与实测（点）土壤含盐量时间序列对比

从图中可以看到，利用反演参数得到的地下水埋深值与实测值比较接近，在几个极值点都吻合良好，决定系数R2达到了0.98，RMSE值为6.136cm。剖面的土壤含水量模拟值和实测值之间也较为接近，尤其是较好地模拟出了表层土壤含水量的变化；在整个反演时间序列中，2007年11月10日至2007年11月16日（此期内发生了一次灌水和一次降雨）的含水量变化模拟效果较好；反演期间各层的土壤含水量的RMSE值为反演得到的土壤含盐量与实测值之间有一定的偏差，但整体的趋势比较符合，由于土壤盐分的空间变异性比较大，因此结果也相对可以接受。表6-2给出了反演得到的土壤参数（*为反演中得到的水分参数）。

表6-2　反演得到的土壤参数