暗管排水地段地下水向暗管的流动为二维饱和-非饱和的水体流动，一般而言，地下水位以上的非饱和带的土壤水分运动可以近似看做一维流动。刘培斌等（1999）采用流网与一维模型相结合的方法模拟了排水地段的二维溶质运移问题，且取得了较好的效果。

田间排水条件下的水分与溶质运移问题，可以采用DRAINMOD、RZWQM等具有暗管排水模块的模型来进行研究。但对于大棚覆盖条件下的田间水分运移情况，由于塑料薄膜的覆盖，导致田间的均匀降雨条件被破坏，因此形成了较特殊的水分入渗形式，通过分析田间降雨后侧渗的水分运动形式，期望找到一种对侧渗的简便解决方法，并将这种简化方法与RZWQM模型进行结合，并利用RZWQM模型对溶质运移精确描述的优点，对大棚条件下的水肥盐运移规律进行分析。

对大棚降雨时的侧渗情况进行简化；并将下边界处理为隔水边界，以利用对区域内进行简单的水量平衡计算来分析棚内外水量的交换过程，因此可以表示为如图5-33所示的边界条件。

为了对大棚降雨时的侧渗问题进行分析，得到棚内外的水量交换情况，以用到RZWQM模型中。首先分析了在稳定入渗水量为0.5cm/hr的情况下的水分运动情况。图5-34给出了在每个时段的水流速度的矢量分布，图中左侧箭头标出的为水流由棚外土壤进入棚内土壤的最大深度处（各历时深度分别为21.7cm、35.6cm、46.0cm、60.1cm和77.5cm），右侧箭头标示出的为水流垂直入渗的最大深度（各历时深度分别为25.7cm、43.0cm、58.5cm和77.5cm）；但在t＝10h时，土壤入渗深度达到了模拟区域的最大值（100cm），而发生了水平的水体流动。

图5-33　大棚情况下的降雨边界条件

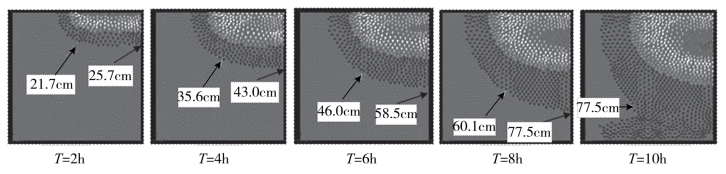
图5-34　大棚侧渗情况下的土壤水流变化图

由于棚外土壤与棚内土壤的长度比例为1∶7，因此两个区域的非饱和带的土壤含水量比较小，则经过降雨以后的水量在棚内棚外的分布应基本相同。如果将降雨量考虑为在整个田间的有效降雨量，则由棚外进入棚内的水分基本应该为均摊在棚内的有效降雨量。

由于在实验区内的暗管埋深一般为80cm深度，因此在降雨量较小的情况下，可能发生如图5-34所示的t＝2h、t＝4h等的降雨量在非饱和位置的入渗，这种情况一般在短时间内（t＜8h）完成；在降雨量较大时，可能发生如图5-34所示的t＝10h的情况，降雨会快速进入饱和水流中，进而发生在非饱和位置和饱和位置的双重交换。(www.daowen.com)

因此，本书提出如下假定：假定进入棚内的水量为均摊到棚内的有效降雨量，这部分水量可以分为两部分进入棚内，一部分在一定的非饱和土壤中进入棚内，一部分先垂直入渗到达地下水位面处，然后再进入棚内。如图5-35所示，非饱和土壤内的棚内外交换水量用右侧三角形表示，垂直入渗后到达地下水位面的水量用右侧方框表示。因此侧渗进入棚内的水量的比例（侧渗分数If）可以计算为：

式中：Lv为垂直入渗的最大深度（即图中的70.80cm）；L为棚外的地面方向宽度（实验区内的为1m）。

图5-35　侧渗深度和垂直深度示意图

为了得到侧渗深度（图5-35中左侧箭头所示位置）和垂直入渗深度（即图5-35中右侧箭头所示位置），采用Hydrus模型计算了在0.25cm/h、0.5cm/h、1cm/h稳定入渗情况下，入渗水量为0.4cm、2.0cm、3.0cm、4.0cm、5.0cm时两种湿润峰的运动深度值。

图5-36　不同入渗水量下的入渗深度分布

从图5-36中可以看出，入渗深度和入渗水量之间具有一定的相关关系。水分入渗以后，水分在土壤内的分布，一般会随着时间的增加而不断地变化，但是对于本文所作的简化而言，一般的降雨都是以天为时段进行分析的，因此在一天以内的变化是可以接受的。故采用以上的简化关系式对侧渗最大深度和垂直渗最大深度进行计算，并得到侧渗的分数。