1.温室内自然通风理论及气流场模型

温室内外由于太阳辐射（Sun等，2016b）、温度差、压差和作物腾发等影响，整个系统的不同部分之间不断进行着空气和能量的交换。温室内外的气候分析发现，室内风速主要受室外风速和温室通风口的共同影响，受室外温度的影响较小，且有研究者认为温室外部来风对室内气流场起主导作用。因此，本书中考虑温室自然通风情况时，没有考虑温室内外的热压作用，为了计算方便，在气流场的模拟中室外风速也采用标准风速1m/s。

（1）温室自然通风理论

Boulard和Baille在只考虑风压影响时给出了通风量与外部风速之间的关系：

式中：ϕv为通风流量，m3/s；A0为通风口的面积，m2；Cd为流量系数（无量纲）；Cw为综合风压系数（无量纲），Cd和Cw系数的取值与大棚的高度和大棚的通风位置有关；V0为温室外风速，m/s。

通过通风量和温室大棚的剖面尺寸，可以得到棚内的风速（Bonlard等，2002）：

式中：Ac为垂直于平均风向的温室横截面积，m2；Vi为室内风速，m/s。上式表明在不考虑热压作用的自然通风情况下，外部风速和内部风速之间存在线性关系。

（2）计算流体力学理论

自然通风条件下温室内空气流速较低，且流动过程中空气温度变化不大，其通风过程可视为不可压缩流体运动，且认为流体在流动过程中遵循基于雷诺时均的黏性不可压的Navier-Stokes方程：

式中：ρ为流体密度，kg/m3；v为速度，m/s；Γφ为广义扩散系数；Sφ为广义源项；φ为通用变量。

温室的自然通风过程具有明显的湍流特征，模拟计算时选用了具有优越的收敛性能和合理的精确度的标准k-ε，假设近壁处气流流动符合标准壁面函数。为了得到整个大棚内的平均风速，对计算结果的处理采用按体积积分的方法，依下式计算：

式中：ui为速度分量，m/s；n为控制容积表面方向的单位向量；fVi为计算的内部平均风速，m/s。

（3）流场模型

实验区栽培生产使用的塑料大棚如图4-14所示，由于相邻大棚间间距较小，且侧窗非夏季通常不打开，因此只考虑了单栋大棚，进出风口为前后山墙门。其几何尺寸为：跨度（沿X向）6m，脊高（沿Y向）2.5m，棚长（沿Z向）50m，进出风口的山墙门尺寸为2.0m×2.0m。模拟时段内假设进出口的山墙门全开，风向夹角为外部风向与Z轴正向的逆时针夹角。

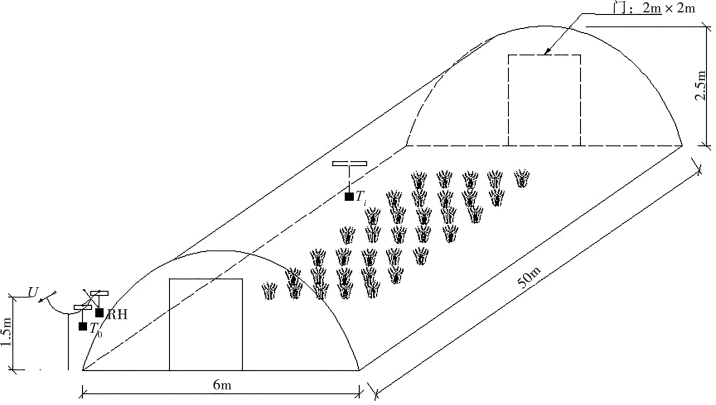
图4-14　塑料大棚模型尺寸和外部气候测量示意图

模拟设定进风口边界条件为速度进口边界，出口采用压力边界条件，参考温度选定为298K（即25℃），计算风速假定为1m/s。建立流场模型时，计算域取为沿宽度方向外延2m，沿长度方向外延10m，模型尺寸为70m×10m×5m。采用非结构四面体网格，在温室进出口处进行加密处理，对计算体共剖分53686个网格。

2.温室作物蒸腾理论

考虑太阳辐射（Sun等，2015a；Sun等，2015b）和温室内外的热量传递，系统的能量平衡可以表示如下[59]：

式中：G0为太阳辐射，W/m2；μ为外部辐射加热效率；Ks与KL为室内外显热和潜热传递系数，W/（m2·K）；Kc为室内外的传热系数，W/（m2·K）；ΔT为室内外的空气温度差，K；Δe为室内外的蒸汽压力差，Pa。

室内外的传热系数Kc一般认为与外部风速V0有关：

式中：A、B为与温室大棚的材料等有关的传热系数，一般取值6和0.5。

温室内外的显热传递系数Ks和潜热传递系数KL可以利用通风流量ϕv表示：

式中：Cp为空气比热，J/（kg·K）；Ag为温室地面面积，m2；λ为汽化潜热，J/kg；ξ为标准温度下的水汽含量和水汽压力的换算系数，一般取值为6.25×10-6kgw/（kga·Pa）。

Stanghellini（1987）建议利用下式计算叶部增温（Stanghellini等，1987）：

式中：rs、ra分别为叶片气孔阻力和空气动力学阻力，s/m；δ、γ分别为饱和水汽压与温度曲线的斜率和湿度常数，Pa/K；ILA为叶面积指数；分别为叶片周围空气的饱和水汽压和实际水汽压，Pa。

温室内空气温湿度的状况会直接受到温室内地面蒸发和作物蒸腾的影响；其中作物蒸腾一方面产生了能量消耗，减缓了温室内空气温度的剧烈上升，同时，蒸腾产生的水汽也使得空气湿度增大。在对温室内空气温湿度和作物蒸腾、地面蒸发等的研究中，由于地面蒸发量占总的腾发量的比例较小，一般都认为在正常的水分管理条件下的温室内腾发量约等于作物蒸腾量。由紊流扩散方程计算作物蒸腾量时存在下式：

式中：为叶温下的饱和水汽压，根据空气-饱和水汽压的关系，有：

若不考虑温室内水汽的压缩性，室内的蒸腾产生的水汽应等于室内外的水汽流量：

(www.daowen.com)

综合以上表达式，可得（孙怀卫等，2011）：

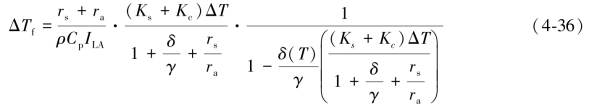
式中：叶片气孔阻力（rs）和空气动力学阻力（ra）根据Boulard的研究结果（Boulard，2002）和戴剑锋的处理（戴剑锋等，2006），可通过温室内作物参数dv（叶片的特征长度，m）和G0、Vi计算：

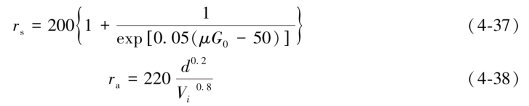
由于温室内冠层部分在日间接受太阳辐射，冠层叶部升温所需要的能耗组成了温室内单位时间的热储项的变化，可以表示为（Papadakis等，1994）：

式中：w为单位面积（1m2）上的作物物质量，kg；Cc为作物比热，J/（kg·K）；ΔTf为叶部与周围空气温度差，K。

根据式（4-36）所求的叶部温度与空气之间的差ΔTf，可以计算得到作物的蒸腾量：

3.模拟结果与蒸腾量验证

（1）温室气流场特征及通风参数

为了分析在不同的外部风向下温室内的气流场变化情况，取主向为与大棚屋脊平行向南（见图4-14），按风向角θ从0°～90°变化，逐次模拟分析了15°、30°、45°、60°、75°等夹角下外部风速1m/s时室内风速变化。图4-15给出了一定夹角情况下（以75°为例）水平方向上平均室内风速沿大棚中轴线分布图。

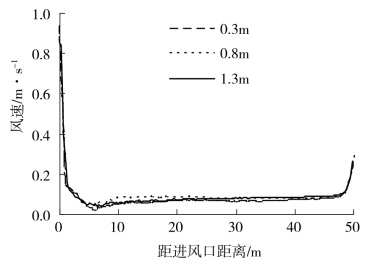
图4-15　距地面0.3m、0.8m、1.3m高度处水平方向速度分布图

从图4-15中可以看出，风速在进风口开始逐渐降低，从1m/s降低到一个较低的稳定值，随后在出风口处又呈上升趋势。在不同的风向下，棚内风速和风速的水平分布有明显不同；但在温室进风口处出现了程度不同的风速剧烈变化带，且风速温度段都集中在温室中央部分，风速平稳区占整个棚长的比例都超过了70%。有研究中指出，温室内的气流场特征与不同的窗口布局有关，也与温室形状、进风风向等有关（Boulard等，2002），此计算结果给出了适合上海地区的塑料大棚的自然通风特征。

为了计算整个温室内的作物蒸腾量，根据气流场变化特征，如果选择温室内的风速平稳区风速进行计算，基本可以代表温室内的气流特征。由此，需要选择一个合适的棚内风速指标来计算与气流场有关的空气动力学阻抗等参数。

为了获得温室自然通风的理论参数，使计算结果可以运用在同类温室的作物蒸腾量的计算中，同类研究中大多通过试验和CFD的模拟建立了内部风速和外部风速之间的定量关系，如Wang等通过分析温室的通风口的开启角度α和内部风速之间的关系（汪小旵等，2007）。根据温室内气流场模拟结果分析了外部Z向进风速度、外部风向角度和按照式（4-29）计算的内部矢量平均风速和Z向平均风速之间的关系，见图4-16。其中外部Z向风速（Voz，m/s）采用下式进行计算：

式中：Vo为外部风速，m/s，在气流场的模拟过程中，采用的为标准风速1m/s；θ为外部风向与大棚Z向（沿大棚屋脊方向）的夹角。

图4-16　内部风速与外部Z向风速Voz和外部风向角度θ之间关系

结果表明，棚内矢量平均风速Vi（图4-16（a））与外部Z向风速Voz高度相关（R2＝0.954），棚内Z向平均风速Viz（图4-16（a））与外部Z向风速Voz正相关（R2＝1）；棚内矢量平均风速Vi（图4-16（b））与外部风向角度θ相关（R2＝0.823），棚内Z向平均风速Viz（图4-16（b））与外部风向角度θ（R2＝0.93）。由以上结果，温室内部的Z向平均风速和外部的Z向风速之间存在较好的线性关系，按照温室内的自然通风理论公式，根据棚内外的风速关系可以求得自然通风的参数值。

（2）验证资料

田间试验在上海市青浦区水利技术推广站的基地试验大棚内进行。温室尺寸即气流场模拟模型尺寸，大棚内试验作物为当地韭菜，种植行株距为20cm×20cm，种植中韭菜每隔30～40天收割一次。试验中室外气象参数来自大棚附近的试验站气象场，室内采用温度计测量了室内温度。植株蒸腾量的测量，通过称重法每天8时采用60kg±2g的电子天平测量，所使用的2个测桶（D＝29cm）对称分布于大棚的轴线两侧，由于在试验中控制测桶内的植株覆盖良好，按照前述论述，认为电子天平的两次读数之间的差值即为作物的蒸腾量。试验期间测量了植株的生长高度，2008年3月27日开始试验时植株高度为31cm，4月21日收割时将作物割至地面以上2cm处，试验在2008年5月结束，实验中测量得到1m×1m面积上的作物最大收获量10kg，平均的作物收获量为4kg，因此认为单位面积的作物物质量为w＝4kg。

本书中的太阳辐射照度由外部的气象条件算得；温室大棚内的辐射加热效率μ，根据在相同地区的普查资料，大棚透光率为0.53±0.07，结合使用ZF-2型照度仪的测量结果，本文取值μ＝0.51；由以上的大棚内自然通风理论计算求得通风参数为0.327，并利用气象站提供的风向、风速数据（测量点距离地面1.5m高度）进行计算。根据式6-18计算出试验期间的逐日作物蒸腾量和累积蒸腾量与实测结果的比较，如图4-17所示。

图4-17　逐日蒸腾量和累积蒸腾量模拟值与实测值的比较

从图中可以看出，通过CFD技术模拟后确定的参数结合能量平衡及蒸腾量计算方程，模拟的温室大棚内作物的逐日蒸腾量与实测值间趋势吻合良好（R2＝0.776），在试验期间的实测作物累积蒸腾量与计算作物累积蒸腾量相差不大，基本分布在1∶1比例线附近（R2＝0.998，标准误SE＝1.16mm，与实测值之间最大绝对误差为4.82mm）。试验期间由于计算中采用的进入温室内的辐射为利用常规气象计算及测量室内温度也可能存在一定的偶然误差等，造成了计算的逐日蒸腾量与实测数据之间的表现没有累积蒸腾量吻合的好。图4-17中累积蒸腾量的计算值和模拟值非常接近的结果也表明，利用本文所建立的方法，在长期的水管理的计算中的误差比较小，可以满足水资源管理、温室规划等方面的需求。

为了分析在逐日蒸腾量的计算中，风速、日照时数、室内外温差等因素对于计算方法的影响，按每天实测的这三个指标相对于平均值的大小（试验期间的平均风速为1.4m/s；平均日照时数为4.5h；平均的室内外温差为2.9℃），比较了计算所得的逐日蒸腾量和实测值，计算结果见图4-18。从图中可以看出，不同的气候因子对于蒸腾量计算的影响不同，本书中考虑整个系统的能量平衡时，对室内外的能量交换和水汽交替做了一些简化，因此在室内外温差较小（小于平均温差2.9℃）、外部风速较小（小于平均风速1.4m/s）和日照时数较小（小于平均日照4.5h）时，计算值与实测值之间吻合程度较差。

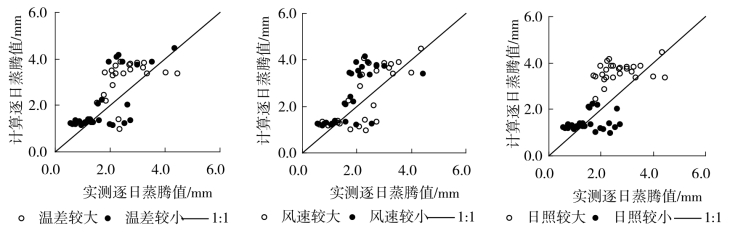
图4-18　逐日蒸腾量与三个主要的影响因子之间的关系

（3）作物蒸腾量计算敏感性分析

为了检查作物蒸腾量计算模型中参数对于模拟结果的影响，对模型中的参数进行了敏感性分析。敏感性系数Sx定义为：

式中：代表每次分析的参数x，s代表衡量指标变化的比例。通过敏感性系数Sx，可比较不同参数间的敏感性。对于每个变量的敏感性分析，本书通过考虑将模型方程的参数值上下变动20%后累积蒸腾量的值相对于试验测定累积蒸腾量值的变化，按照式（4-42）计算了各个参数的敏感性。表中列出了对参数等做敏感性分析后的结果。

表4-10　简单计算模型中不同参数的敏感性分析

表中Sx值越大，参数在蒸腾量的计算中越重要。辐射加热效率μ（即透光率）对应的Sx为2.14%，随着μ取值的增加（合理值0.46～0.61），作物蒸腾量增大；温室通风的经验参数的改变对蒸腾量的计算有一定的影响，根据CFD技术模拟确定参数可以提高蒸腾量计算的精度。蒸腾量计算精度对辐射加热效率、显热交换系数等与辐射有关的参数取值较为敏感，说明温室内作物蒸腾量的主要能量来源于太阳辐射，罗卫红等的研究也表明作物蒸腾消耗的能量占进入温室能量的一半[64]；这同时也说明在建立经验参数模型时需把握太阳辐射项为影响蒸腾量的主要因子，利用实测数据或经过验证数据进行计算，以避免计算中产生较大误差。