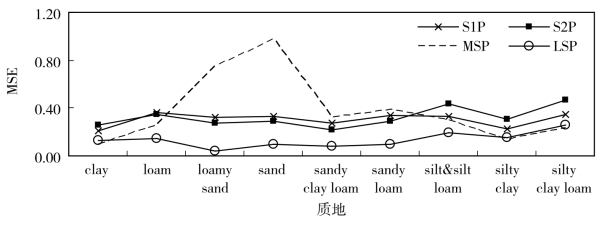
图4-5　不同质地情况下平均MSE表现

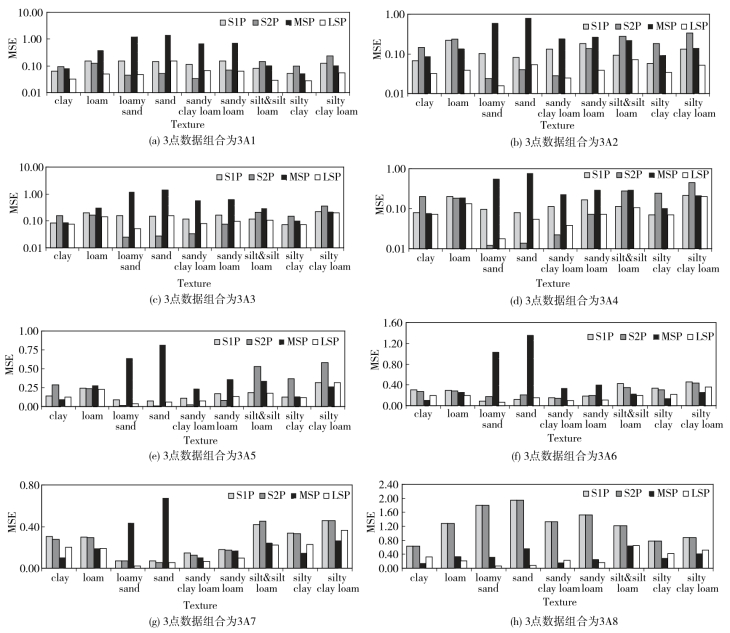
图4-6　不同土质4种方法的拟合效果分析图

田间持水量被定义为土壤在降雨或灌溉后以悬着水状态所能保持的水分最大值。田间持水量一般被认为是土壤所具有的水分物理性质，也是水利工程设计、作物精量灌溉、土壤水分转换研究和土壤研究等实际应用中的一个关键参数。合理估计田间持水量在农业、水文、水利、环境和地球科学中都有着很重要的意义。田间持水量的确定过程中需要判断土壤是否达到田间持水量的状态，根据判别过程中所依赖的指标，通常将田间持水量的确定方法分为时间法（time-based）、压力势法（pressure-based）和流量法（flux-based）。本书在研究中采用来源于中国的土壤样本数据，对确定田间持水量的数值模拟方法进行了分析和比较，提出了一种较为适合的土壤田间持水量的确定方法。

1.研究样本

研究样本主要为在土壤调查文献中收集到的数据，取样地点包括黑龙江省、安徽省、河北省、云南省、江西省、宁夏省、陕西省、上海市和北京市等，有效样本数为160个。

土壤数据一般包含了土壤的累计粒径分布、土壤的有机质、土壤的容重和土壤在土层中的位置。研究中通过traingle程序（Aris Gerakis，2001）按照土壤的sand和clay含量计算了土壤的质地。土壤样本数据的筛选中，将是否具有良好的土壤颗粒分级数据、田间持水量数据作为选择的标准，同时对田间持水量数据的测量方法一般要求为田间实测值（即围框法），少量数据在文献中的记载没有给出明确的测量方法，但以一定深度的土体所具有的田间持水量来表示，这也被认为是田间实测获得值。在本研究中所包含的土壤数据样本的物理属性中，一般采用吸管法（pipette method）来测量得到土壤的颗粒等级数据；采用环刀取原状土烘干后测量土壤的干容重；采用Walkey-Black方法测量土壤的有机质含量，其中要用到的转换常数取值为1.724。土壤的颗粒等级数据在不同分级标准（国际制、美国制度等）的转换中，由于很多实验数据和文献资料中仅有3个颗粒等级数据，一般应用第4章的推求方法来进行转化。

2.数值法计算田间持水量的理论方程（LOSS）

田间水分运动过程可以用Richards方程来表示。一个一维的Richards方程的数学表达式为：

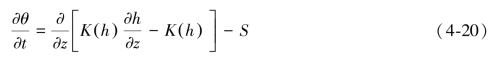
式中：θ为体积含水量；h为压力水头（L）；z为垂向坐标（L）；t为时间（T）；K（h）为非饱和水力传导度（LT-1），一般为h和θ的函数；S代表源汇项。.

函数K（θ）和h（θ）分别为土壤的水力传导函数和水分特征曲线：

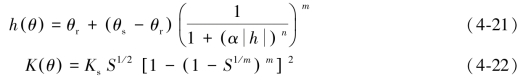
式中：θr为土壤残余含水量；θs为土壤饱和含水量；α为土壤进气值压力；m和n为拟合参数，且一般假定为土壤饱和度；Ks为饱和土壤导水率。

3.土壤的传递函数

表4-7中列出了研究中所采用的7种PTFs的输入数据要求，并列出了不同的土壤传递函数的颗粒分级数据所采用的颗粒分级标准。大多数的土壤PTFs都采用了美国制的土壤颗粒分级标准，但Minasny和McBratney（2003）和Li和Chen（2007）两个PTFs采用国际制的颗粒分级标准，其中Minasny和McBratney（2003）的输入变量中，如果将sand含量（20～2000um）按照Fine sand（20～200um）和Coarse sand（200～2000um）分成两类进行输入，可以提高PTFs的预测精度。Wösten（1999）的输入变量包含了土壤样本在土层中的位置（Topsoil/subsoil），这部分数据依照土壤样本中对土壤剖面的描述来确定。在这6个PTFs模型中，除了Zacharias和Wessolek（2007）仅能给出土壤水分特征曲线的参数而不能给出土壤的饱和水力传到度Ks以外，其他6个模型都能够给出完整的van Genuchten-Mualem模型参数值。因此，依据Ferrer建立关于Ks的回归等式时所具有的饱和水力传导度数据样本数最多，选择Ferrer单变量模拟的Ks值与Zacharias和Wessolek（2007）的输出值结合来组成完整的van Genuchten-Mualem模型参数。

表4-7　用来计算水力参数的传递函数（PTFs）

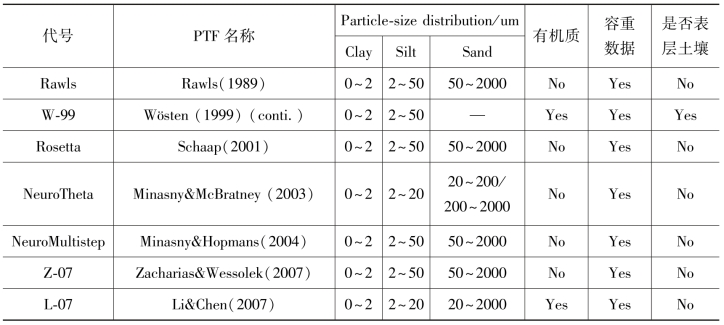
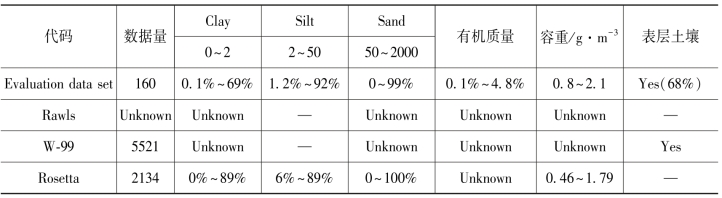
表4-8中列出了7个PTFs建立时所用到的土壤样本和本研究用来评估的土壤样本的颗粒等级分布情况、有机质情况和容重资料。从表中可以看出，除了NeuroMultistep软件和L-07两个PTFs由于所包含的土壤样本数据较少而相对于评估数据库的Clay和Sand范围略小以外，其他的PTFs基本都能满足要求；但是Rosetta PTFs建立时的土壤样本中没有包含silt很小的土壤样本。同时由于用来评估的土壤样本来源比较多，造成样本的有机质含量和容重范围都比较大，相比于一般的PTFs建立的土壤样本特点要更加大一些。

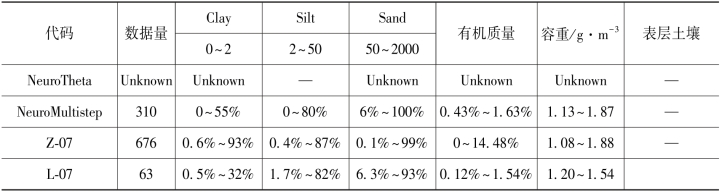
表4-8　传递函数的适用范围和需要输入的数据类型（PTFs）

续表

(www.daowen.com)

为了评价不同方法和传递函数下数值模拟值和实测值之间的差异，采用了Kobayashi and Salam提出的MSD指标和决定系数R2来进行评价。

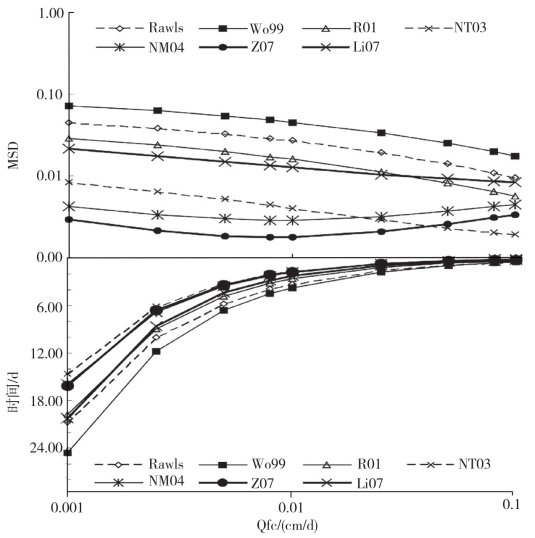
图4-7　不同流量阈值Qfc下模拟田间持水量的MSD和达到阈值的时间Tfc

4.田间持水量的下渗流量阈值

为了确定合适的田间持水量的下渗流量阈值Qfc，分别计算了在不同的Qfc达到时的土壤含水量为田间持水量，并比较了与测量值之间的差异。从图4-7中可以看出，Wo99、Rawls、R01和Li07等PTFs的MSD值相对偏大，说明这4个PTFs的表现相对较差；NT03、NM04和Z07的MSD值比较小，且Z07的表现最优。在表现较好的Z07和NM04中，当Qfc取值为0.008cm/d和0.01cm/d时，计算所得的MSD值最好。可以看出，随着Qfc的取值逐渐的减小，达到Qfc的时间也逐渐增大，Qfc＝0.005cm/d时平均达到Qfc的时间要比Qfc＝0.025cm/d多2.4d。同时也可以看到不同的PTFs计算达到Qfc的时间没有很大的不同。在图中，也可以看到，虽然R01、NT03等PTFs在Qfc＝0.1cm/d时具有较小的MSD值，但是计算达到Qfc的时间都比较小，这与实际情况不是很吻合的。在Qfc取值为0.01cm/d和0.008cm/d时，达到Qfc的时间与传统经验值较为符合。

根据以上分析，数值模拟计算田间持水量时，采用Qfc取值为0.01cm/d和0.008cm/d时，土体模拟计算达到Qfc时需要的时间与传统测量较为符合。当采用NM04和Z07两个传递函数计算土体的水力参数属性时，在Qfc＝0.005～0.025cm/d也取得了最小的MSD值。研究还表明，采用特定内排水历时作为是否达到田间持水量的条件，也可以获得较为稳定的田间土壤含水量的参考值，但是对于不同的土壤，达到稳定的田间土壤含水量状态的时间还是存在较大的差异。因此，采用下渗流量作为田间持水量是否达到的条件要优于内排水历时的判断，选自流量阈值为Qfc＝0.01cm/d作为达到田间持水量的下渗流量计算要优于内排水历时。

5.适宜的土壤传递函数

按照不同的土壤质地，对R01、NT03、NM04、Li07和Z07传递函数在模拟田间持水量上的表现进行了分析，结果如图4-8所示。

从图4-8中可以看出，Li07在质地为clay和silt clay的土壤上对田间持水量有明显的低估；R01在质地为clay和sand类土质上表现较好，但是在silt＆silt loam、silt clay和silt clay loam等土质上对田间持水量有所低估。图4-9中还给出了NT03、NM04和Z07 3个表现较好的PTFs对所有土壤的拟合情况，可以看出，NT03对于土壤的拟合更趋于分散，NM04在拟合中有少许的离散点，Z07的拟合效果最好；3个PTFs的估计值与测量值之间的决定系数R2分别为0.5367、0.6637和0.6833。这说明采用Z07的传递函数作为模拟土壤含水量的传递函数，能够获得与测量值较好的吻合。

对上述传递函数的比较也发现，采用将有机质作为变量建立的传递函数如Wosten（1999）、Li07等相对于Rosetta、NT03、NM04等并不具有明显的优势。利用不含有机质变量的PTFs推求土壤的水力属性参数，也可以建立土壤的田间持水量依土壤质地变化的关系。

6.田间持水量的特性分析

按照土壤中的silt含量和clay含量以2%的量变化，并假设土壤的容重值变化范围为1.1～1.7g/cm3，计算土壤的田间持水量依土壤质地的变化情况。图4-9列出了在土壤的容重为1.3g/cm3、1.5g/cm3和1.7g/cm3时土壤的田间持水量的分布图。

通过与Ad-Hoc-AG Boden（2006）的土壤调查数据比较，模拟所得的田间持水量整体分布吻合较好，但在clay含量为10%左右时，数值模拟对田间持水量有所低估。造成这种现象的原因有：（1）田间实测值时土壤大多位于土层的某个位置处，但是在数值模拟中，没有考虑上下层土壤对土壤的田间持水量的影响；（2）通过中国土壤数据库选择的PTFs函数可能在小范围内不太适应于德国的土壤实际情况。

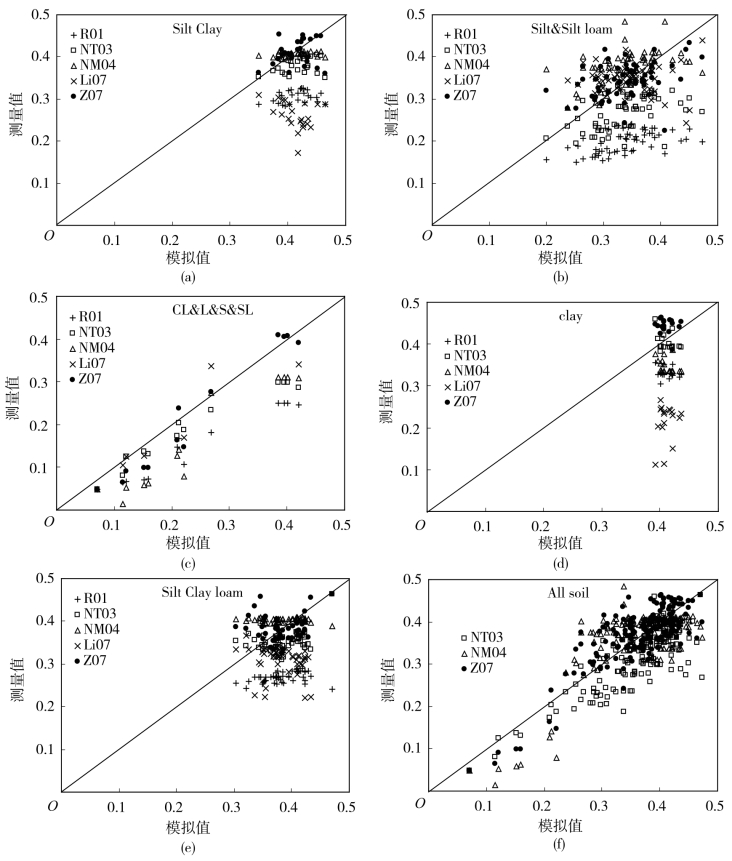
图4-8　不同传递函数下的数值模拟方法效果

有很多学者建立了根据田间持水量与土壤质地、容重等之间的关系，并提出了一些较好的回归函数用来计算土壤的田间持水量、土壤的有效水量等。但是，根据田间实测的田间持水量来建立回归等式时，可能遇到的一个问题是土壤数据库样本偏小或不足。通过数值模拟方法在不同的容重情况下土壤田间持水量依土壤质地变化的数据库，可以快速获得大量的土壤样本数据。首先，对田间持水量与土壤质地、容重之间的相关关系进行了分析，相关关系图如4-10所示。

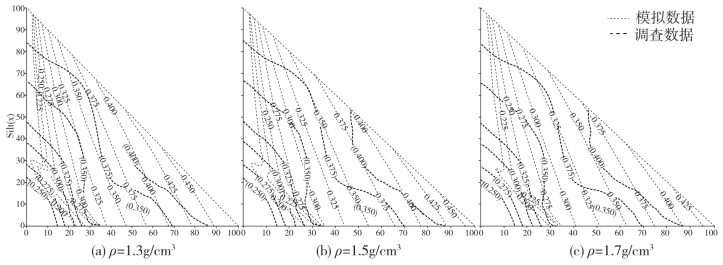
图4-9　不同容重下的田间持水量的变化

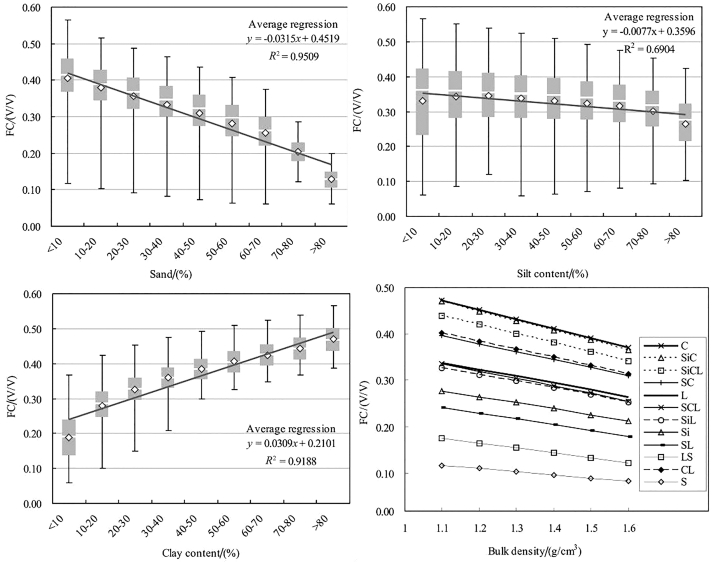
图4-10　田间持水量（FC）与不同颗粒数据和容重的关系

从图中可以看出，土壤的田间持水量与sand、clay含量等有密切的关系，这在一些回归函数中也有所体现。同时，在同种土壤质地下，土壤的田间持水量和容重之间，近似于直线关系。一般而言，土壤的田间持水量随着土壤砂黏含量的增加而呈现下降趋势，而随着土壤黏粒含量的增加而增加，同种质地情况下，土壤的田间持水量随着容重的增加而降低。

研究结果表明：对田间持水量的确定过程采用Hydrus 5.0进行数值模拟，并选用了7个合适的土壤传递函数（PTFs）：Rawls PTF、Rosetta PTF、NeuroTheta PTF、Neuro Multistep PTF、Zacharias PTF、Li和Chen PTF、Wösten PTF用来获得模拟中所需的土壤水力参数；通过选用均方偏差（MSD）来比较实地实验和估计所得的田间持水量之间的差异大小，对田间持水量的时间法和流量法进行了比较。结果发现，采用0.01cm/d的特征流量能够获得与田间试验结果较为接近的田间持水量模拟值，Z07 PTF和NM04 PTF都提供了较好的模拟效果，采用Z07 PTF的适应拟合土壤质地，绘制了土壤的田间持水量依质地变化图，并发现按照这种方法绘制的土壤持水量分布图更接近已有的土壤调查资料。最后，根据按照数值模拟方法建立的土壤田间持水量数据库，分析了田间持水量与土壤的质地、容重数据等之间的相关关系。