土壤的颗粒分布数据是土壤研究中一个比较重要的参数。近年来，对土壤颗粒分布模型研究的开展，基本满足了在不同条件下有较多个测量粒径组成的数据时对土壤颗粒分布曲线估计的要求。但是对仅仅具有砂粒、粉粒和黏粒3个含量数据的情况下，合理估计土壤颗粒分布曲线的研究开展的还比较有限（Skaggs等，2001）。

利用砂粒、粉粒和黏粒含量数据估计完整颗粒分布的基础是Skaggs（2001）发现有下列线性关系式的成立：

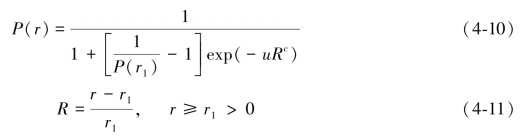
式中：P（r）为对应土壤粒径r的土壤累积颗粒分数；r1为模型应用的最小土壤粒径；c和u为模型参数。一般称同时具有c和u等两个模型参数的模型为S2P模型，如果将c值固定为1时，可以称为S1P模型。

为了求解两个参数c和u，公式可以转化为：

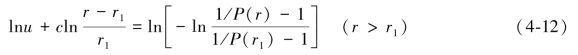
因此c和u分别可以利用下面的式子来进行求解：

式中：1＞P（r3）＞P（r2）＞P（r1）＞0，r3＞r2＞r1＞0，

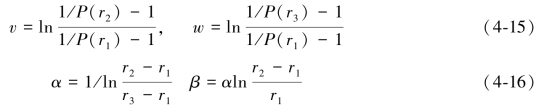
因此，可以根据P（r1）、P（r2）、P（r3）来求解参数c和u。采用S1P模型根据X（0）（1）和X（0）（2）（X（0）（i）为待估计数据对）来预估得到一个对应于半径r0的X（0）（0）（r0＜r1）。利用r0代替r1，可以得到下式：

如果假定待进行完整颗粒曲线估计的质地数据（记为ITL，X（0））为：

则可以对待进行完整颗粒曲线估计的质地数据（ITL）进行拓展。采用同样的方法，计算对应半径r4的X（0）（4）（r3＜r4），并将ITL数据拓展如下：

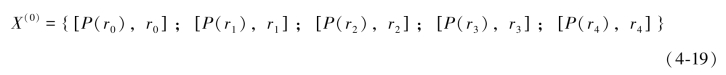
按照式，对整段PSD曲线进行分段线性求解，可以得到r1～r2，r2～r3，r3～r4等分段区间的S2P计算参数{c1，u1}，{c2，u2}和{c3，u3}，并可以依据这些参数计算整段PSD的数据。

为了与S1P和S2P进行区别，称这种分段线性的PSD分析方法为LSP方法，与S1P、S2P方法进行比较，同时还与经常采用的正态插值法（MSP）一起进行了比较。采用了4个经常使用的评价指标MSE、MAPE、AAE和R2来对以上几种方法在数据估计上的表现进行评价。(www.daowen.com)

首先选择了UNSODA数据库中236个土壤数据样本进行了分析，所有选择的土壤样本的测量粒径数都大于6个，同时具有几个关键粒径如0.002mm、0.02mm、0.05mm、0.1mm和0.2mm等，大致的粒径范围都为0.002～2mm。对于少数的土壤样本数据，可能实际测量的粒径不包含了几个关键粒径只有比较小的偏差如0.016mm，这时数据需要根据相邻两个测量数据利用插值的方法生成在关键粒径位置的数据。为了检验以上提出的4种方法的优劣性，假设在以上选择的UNSODA数据库样本中，每个样本只有3个已知的粒径数据，然后利用这4种方法来进行计算和估计，并将估计的数据与实际测得的多点的数据做比较。如果根据3点估计出来的数据与实际测得的多点的数据之间的偏差比较小，这就说明可以仅仅利用3点的数据就得到与测量数据差不多的信息了，也说明了该方法是可靠和适用的。

因为土壤的分级标准比较多，例如中国的土壤研究中采用的分级标准就同时存在卡庆斯基制、美国制和国际制等，还有一些其他的分级制标准（Nemes等，1999）。为此，我们根据数据情况，拟定了8种可能的3点颗粒的组合，见表4-6。在下表列出的8种组合中，3A1组合的3种粒径与Skaggs提出的粒径组合接近；3A1～3A5的最小粒径为0.002mm，3A6、3A7的最小粒径为0.02mm，3A8的最小粒径为0.05mm。

表4-6　用来进行颗粒分布估计的3点数据的组合假设（单位：mm）

图4-2给出了利用S1P、S2P、MSP、LSP 4种方法对来自UNSODA数据库的土壤样本进行计算的流程图，以3A1为例。

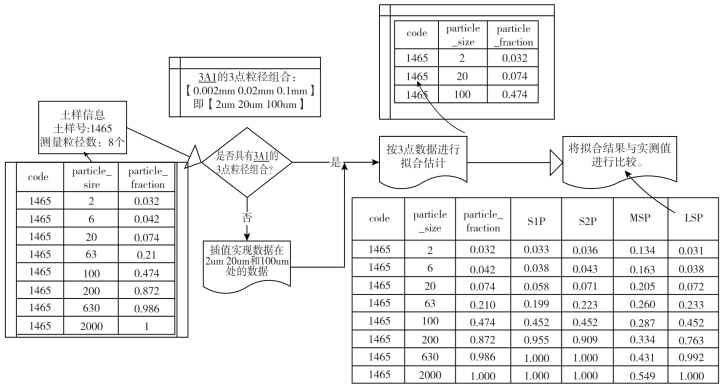
图4-2　计算过程流程图

对于8种不同的3点粒径组合而言，可能存在的情况是如果应用S1P和S2P方法中的一些关键点的缺失，造成拟合中曲线形式变化，从而造成很大的误差。为此，可能这4种方法在不同的3点粒径组合中的表现不一。图4-3给出了这8种组合情况下采用这4种方法计算时几个误差指标的变化。

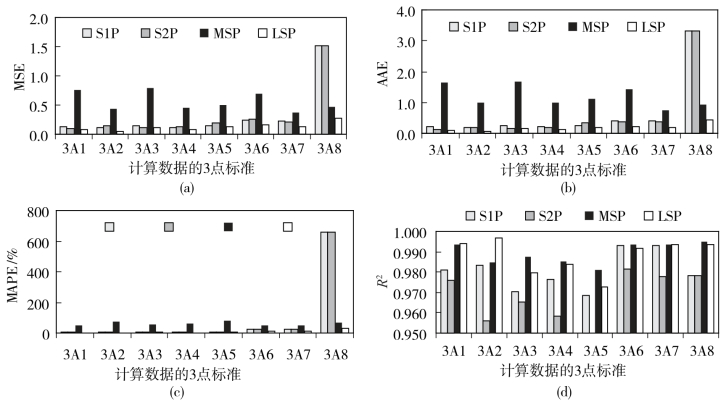
图4-3　不同颗粒组合情况下的误差指标的变化图

从图中结果看到：对于4种针对有限数据进行拟合的方法进行比较，可以发现LSP方法最佳，方法造成的误差MSE从0.080变化到0.266，相对误差范围为2.1%～29.0%。造成S1P和S2P在拟合3A8时误差比较大的原因可能是3A8组合的3点数据中最小粒径为0.05mm，这可能造成3个点连接的曲线形式与Skaggs模型的曲线形式相差比较大，从而造成拟合的误差。S2P与S1P方法的函数形式相似，且在S2P函数的第二参数c＝1时，函数形式就与S1P函数相同。但是在某些土样上的表现，S2P的拟合误差要大于S1P的拟合误差，造成这种情况的原因是根据已知的3点的数据得到的曲线形式与实测的曲线形式间相差比较大，虽然按照S2P方法拟合能够更加接近已知的3个点数据，但在整个完整的粒径分布中表现不佳。反而按照S1P曲线形式，将完整的粒径分布限制为标准的生长逻辑曲线，在一些土壤样本中粒径分布朝未知的粒径分布拓展时，造成的误差更小。

在这4种方法的使用中，整体而言，应该选择LSP方法更为适宜。但是如果对于特定的土壤样本，按照3点数据来进行估计时，造成的误差过大，可能直接影响了方法的实用性，或者说方法的应用范围受到了极大的限制。为了说明这个问题，图4-4给出了这4种方法在不同的组合情况预测的相对误差的分布情况。

从结果中可以看到，最适宜的3点数据来推求土壤的粒径分布曲线的组合依次为：3A1（[0.002，0.02，0.1]）和3A2（[0.002，0.02，0.2]）；3A3和3A4、3A5的预测效果也可以，3A6、3A7和3A8的预测效果比较差。LSP方法在预测时，对于3A1、3A2、3A3、3A4的组合下对75%的样本的数据误差小于5%；在预测3A5、3A6、3A7的组合下超过70%的样本预测误差小于10%；预测3A8组合时超过50%的样本误差小于20%；这说明了LSP方法预测3点数据的可行性和优越性。

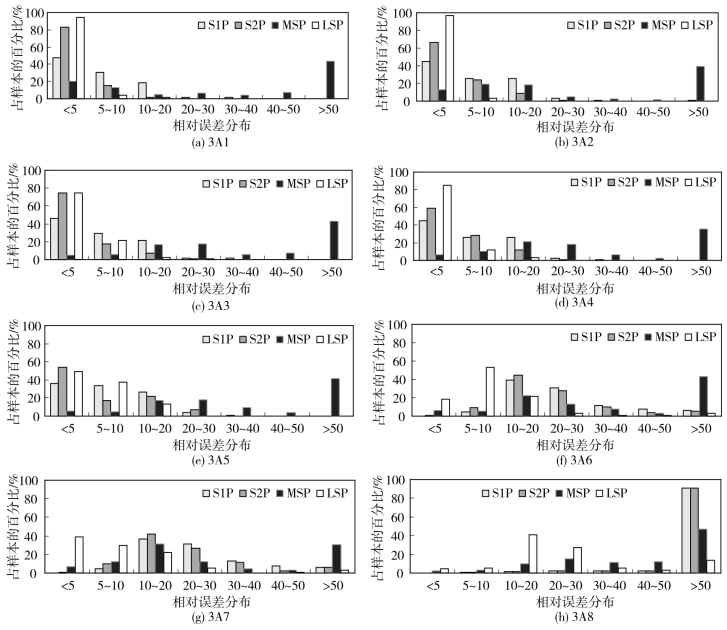
图4-4　不同组合情况下4种计算方法的相对误差分布图

所提出的LSP方法也解决了在Skaggs（2001）的研究中明确指出的对于silt类型的土壤的不适用性；在研究中发现，对于某些silt类的土壤，采用S1P方法进行拟合，可能得到比S2P方法更好的预测效果。因此，下面分析了在不同的土质情况下，采用4种方法进行拟合的效果，见图4-5和图4-6。