功能区划、水质标准、设计水量、数学模型是水环境容量计算必须包含的四大基本要素，也是水环境容量计算的基础。通过功能区划确定区域水体治理的发展方向，并据此确定相应的水体治理控制标准，设计水量的研究是引清调度目标的主要实现任务，也是一个演算的反问题，数学模型的选择则是一个关键。

目前国内外河流环境容量计算方法，以采用静态水质数学模型进行计算分析为主，获得的是一定水文条件下满足水质标准的平均纳污能力。对于水利控制片而言，本书也拟采用这种方法。根据水体自净的特性，水环境容量可分为稀释容量、迁移容量和净化容量三个组成部分。其表达式为

WT=Wd+Wt+Ws

式中　WT——水环境对污染物的容量；

Wd——稀释容量；

Wt——迁移容量；

Ws——净化容量。

具体计算公式为

则

对于黄浦江等外河，具有一定的感潮功能，则需要进行水体动态环境容量的研究。作者以黄浦江水动力学、水质模型为基础，采用最大环境容量方程式进行动态环境容量的计算和分析。

最大环境容量方程式计算条件的基本假设为：

（1）入河污染物的衰减为非线性。(www.daowen.com)

（2）河流二岸为均匀排污。

（3）每个河段的降解系数和沉浮系数为常数。

以COD为例，参与水质模型过程计算的基本算式为

当n→∞，Δti→0时，上式变为

W=86.4(CNQN-C0Q0)+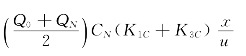

式中　W——河段的环境容量，kg/d；

CN、C0——河段水质标准浓度和河段上断面的初始浓度，mg/L；

QN、Q0——河段末、首断面的流量，m3/s；

u——河段平均流速，m/s；

x——河段长度，m；

K1C、K3C——COD的降解系数和沉浮系数，1/d。