习题1　求下列函数的极限.

习题2　求下列函数的定积分.

习题3　设函数f（x）在[0，1]上连续，且f（x）为非负函数，证明存在x0∈（0，1），使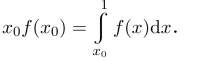

习题6　设

连续，试确定常数a，b.

习题7　在曲线y=lnx上的点（t，lnt）（2＜t＜6）处作曲线的切线，求此切线与直线x=2，x=6以及曲线y=lnx所围平面图形的面积A（t），并求A（t）的最小值.

习题8　在xOy坐标平面中，连续曲线L过点M（1，0），其上任意点P（x，y）（x≠0）处的切线斜率与直线OP的斜率之差等于ax（常数a＞0）.

（1）求L的方程；

（2）当L与直线y=ax所围成平面图形的面积为时，确定a的值.

习题9　已知曲线L的方程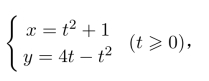

（1）讨论L的凹凸性；

（2）过点（−1，0）引L的切线，求切点（x0，y0），并写出切线的方程；(www.daowen.com)

（3）求此切线与L（对应x≤x0部分）及x轴所围的平面图形的面积.

习题10　在曲线y=x2（x≥0）上某点A作一切线，使之与曲线及x轴所围成图形的面积为，试求：

（1）A点的坐标；

（2）过切点A的切线方程；

（3）该图形绕x轴旋转一周所成旋转体的体积.

习题11　设函数f（x）在[0，1]上连续，且

证明：

（1）存在ξ∈[0，1]，使得|f（ξ）|＞4；

（2）存在η∈[0，1]，使得|f（η）|=4.

习题12　设f（x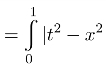）|dt（x＞0），求f′（x）及f（x）的最小值.