【摘要】:18.2.1基本习题讲解例18.1求由参数方程x=acos3t,y=asin3t(0≤t≤2π)所表示的星形线围成的图形的面积.解易知所求面积在第一象限面积内为它的四分之一,即解利用极坐标曲线围成的图形的面积的公式,得到例18.3求心形线r=a(1+cosθ)的长度.解由对称性可知例18.4求y2=2px(0≤x≤x0)绕x轴旋转所得旋转体的侧面积.解 直接利用旋转曲面的计算公式,得
18.2.1 基本习题讲解
例18.1 求由参数方程x=acos3t,y=asin3t(0≤t≤2π)所表示的星形线围成的图形的面积.
解 易知所求面积在第一象限面积内为它的四分之一,即

解 利用极坐标曲线围成的图形的面积的公式,得到
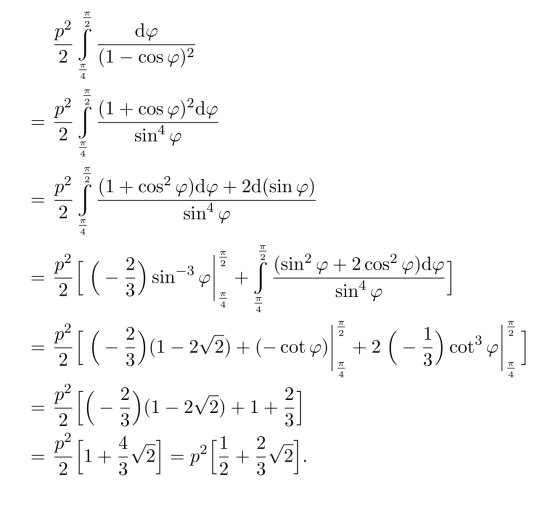
例18.3 求心形线r=a(1+cosθ)的长度.
解 由对称性可知
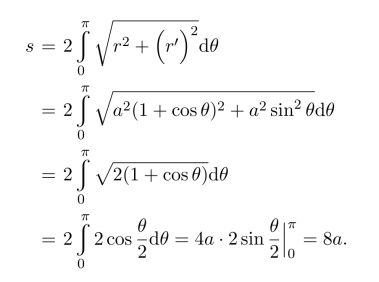
例18.4 求y2=2px(0≤x≤x0)绕x轴旋转所得旋转体的侧面积.
解 直接利用旋转曲面的计算公式,得

求f(x).
解 令u=t−x,则
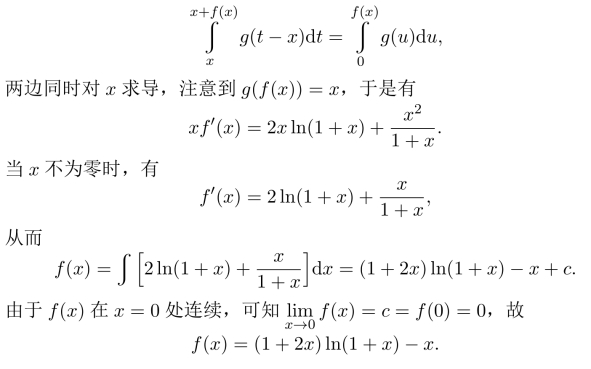
18.2.2 拓展习题讲解
例18.6 求由四条曲线y=x2,y=2x2,xy=1,xy=2所围成的图形的面积.
解 如图18-1,曲线y=2x2与xy=1的交点为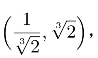 曲线xy=2与y=x2的交点坐标为
曲线xy=2与y=x2的交点坐标为![]() xy=1与y=x2的交点坐标为(1,1),xy=2与y=2x2的交点坐标为(1,2),于是四条曲线所围成的图形的面积为(https://www.daowen.com)
xy=1与y=x2的交点坐标为(1,1),xy=2与y=2x2的交点坐标为(1,2),于是四条曲线所围成的图形的面积为(https://www.daowen.com)
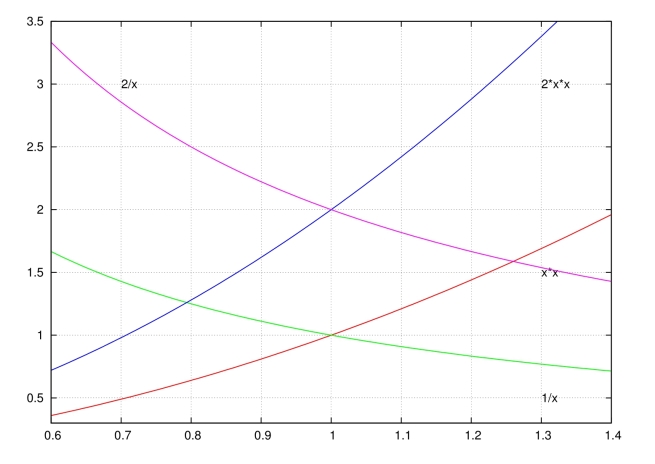
图18-1例18.6的图形
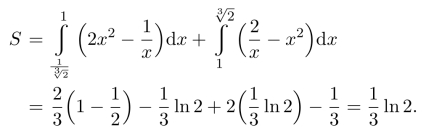
例18.7 过坐标原点作曲线y=lnx的切线,该切线与曲线y=lnx及x轴围成平面图形D.
(1)求D的面积A;(2)求D绕直线x=e旋转一周所得旋转体的体积V.
解(1)设切点的横坐标为x0,则曲线y=lnx在点(x0,lnx0)处的切线方程是![]()
由于该切线过原点知lnx0−1=0,从而x0=e,所以切线方程为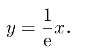

解 用定积分表示旋转体的体积和侧面积,二者及底面积都是t的函数,然后计算它们之间的关系.
(1)利用公式,得
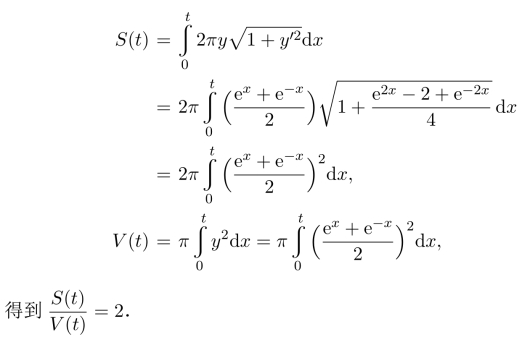
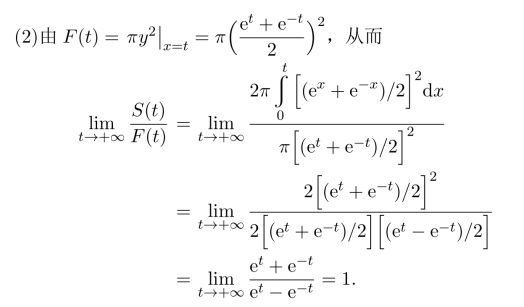
例18.9 将心形线ρ=a(1+cosθ)绕极轴旋转,求旋转生成的曲面面积.
解 由极坐标形式曲线的弧长公式,得
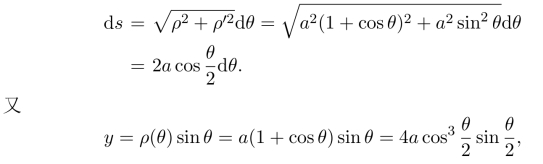
该旋转面面积
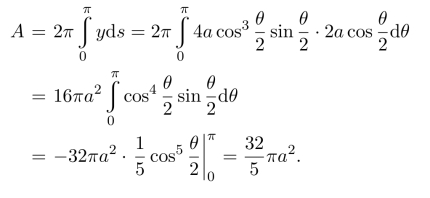
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章







