A组

习题12.1　求曲线x2y=1（x＞0）上任一点切线与坐标轴构成的三角形的两条直角边长的和的最小值.

习题12.2　确定a，b，c使曲线（C）：

在（1，−1）处有拐点且使y在x=0处有极值.

习题12.3　求曲线xy2=1（y＞0）上任一点切线与坐标轴构成的三角形的两条直角边长的和的最小值.

习题12.4　半径为√的圆与x轴相切，并沿x轴滚向抛物线（C）：

问它在何处与抛物线相切？此时圆心的坐标为何？并写出公切线方程.

习题12.5　已知圆柱体体积为V，问底半径及高各为多少时，此圆柱体的全部表面积最小？

习题12.6　设f（x）=nx（1−x）n，n为正整数，

（i）求f（x）在闭区间[0，1]上的最大值M（n）；

（ii）求数列的极限

习题12.7　试证明：当x＞0时，（x2−1）lnx≥（x−1）2.

B组

习题12.8　求函数在闭区间[0，3]上的最大值和最小值.

习题12.9　设f′′（x）＞0，f（0）=0，令g（x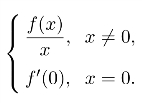）=证明：(www.daowen.com)

（1）g（x）在x=0点连续；

（2）g（x）在x=0点可导；

（3）g（x）在（−∞，+∞）内严格单调增加.

习题12.10　求函数y=xe−x2/4的单调区间、凹凸区间、极值和拐点，并画出草图.

C组

习题12.11　设函数f（x），g（x）具有任意阶导数，且

f′′（x）+f′（x）g（x）+xf（x）=ex−1，f（0）=1，f′（0）=0，则（　）.

（A）f（0）为函数f（x）的极小值；

（B）f（0）为函数f（x）的极大值；

（C）点（0，1）为曲线y=f（x）的拐点；

（D）极值与拐点由g（x）确定.

习题12.12　求函数y=e−x2sinx2的值域.

习题12.13　设任意x，函数f（x）均满足等式

求f（x）的极值.