12.2.1　基本习题讲解

例12.1　设f（x）在[a，+∞）上连续，f′′（x）在（a，+∞）内存在且大于0，记

证明F（x）在（a，+∞）内单调增加.

证明　只需证明F′（x）＞0，x＞a，直接计算，得

由Lagrange中值定理知，存在ξ∈（a，x），使得f（x）−f（a）=（x−a）f′（ξ）.

又由f′′（x）＞0可知，f′（x）＞f′（ξ），所以

证毕.

例12.2　求函数y=x+sinx的凸凹区域及拐点.

解　由于y′（x）=1+cosx=0，得到x=（2k+1）π，k∈Z为驻点.y′′（x）=−sinx在驻点处的函数值均为零.

当x∈（2kπ，（2k+1）π）时，y′′（x）＜0；

当x∈（（2k−1）π，2kπ）时，y′′（x）＞0.所以驻点为拐点，（2kπ，（2k+1）π），k∈Z区域为上凸区域.（（2k−1）π，2kπ），k∈Z区域为上凹区域.

当x＜−1时，y′（x）＜0；

当x∈（−1，1）时，y′（x）＞0；

当x＞1时，y′（x）＜0.

故x=−1，1分别为极小值点和极大值点.

例12.4　求函数y=2tanx−tan2x，0≤x的最大值和最小值.(www.daowen.com)

解　由y′（x）=2sec2x（1−tanx）=0，得到

12.2.2　拓展习题讲解

例12.5　设f（0）=0，f′（x）严格单增，求证函数

在（0，+∞）严格单调增加.

证明　利用导函数的符号可以确定函数的增减性.由

其中利用了Lagrange中值定理，即存在ξ∈（0，x），使得

于是g′（x）＞0，故函数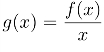在（0，+∞）严格单调增加.

证明　仅证明n=2的情形，因从n=2成立，易得任意的n＞2均成立.

方法一，由于函数下凸，故f′′（x）＞0.对函数f（x1）和f（x2）在k1x1+k2x2处做Taylor展开，得

从而，f（k1x1+k2x2）≤k1f（x1）+k2f（x2）.证毕.

方法二，利用导数的性质来证明不等式，令

则利用G（t）的导数及二阶导数可以证明之（略）.

所以当x＞e时，φ′′（x）＜0，故φ′（x）单调减小，从而当e＜x＜e2时，

即当e＜x＜e2时，φ（x）单调增加.

因此，当e＜a＜b＜e2时，φ（b）＞φ（a），即