7.2.1　基本习题讲解

的极限值均不存在，可知左右导数不存在，故在x=0点不可导.

例7.2　求下列函数的导数.

解　首先注意到，除去x=−1点，函数在定义域上是连续的.

下面考虑在x=±1处的导数.当x=1时，根据导数的定义来求：

所以在x=1处，其导数存在且为

当x=−1时，由于其不连续，故导数不存在（也可以用左右导数验证之）.

所以在x=−1处，函数的导数不存在.

例7.4　设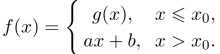其中函数g（x）在x0的左导数存在，问a和b为何值时，函数f（x）在点x0连续且可导.

解　假设g（x）在x0处的左导数为由于函数f（x）在x0连续，故有

由于g（x）在x0的左导数存在，则g（x）在x0点左连续（由左右导数的定义可以证明，或者见拓展习题讲解例7.8），即f（x）在x0点左连续.

从函数f（x）在x0点可导，则其右导数存在，其值为左导数的值.故

故f（x）在x=0处连续.

而

故f（x）在x=0处不可导.

例7.6　思考题：

说明在某一点的右导数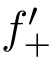（x0）和导函数在某一点的右极限f′（x0+0）之间的不同意义，并结合不同的例子给予说明.

解　由定义，二者区别为：

•前者表示f′（x）在x0点的右极限，后者表示右导数.

•前者定义要求，存在正数δ＞0，使f（x）于（x0，x0+δ）内可导；后者无任何可导性要求.

•前者对于f（x）在x0点是否有定义无关，后者要求f（x）在x0点右连续.有趣的是，导数的右极限有结果：

存在.（读者自己证明）

二者联系：设f（x）于[x0，x0+δ]上连续，在（x0，x0+δ）内可导，如果f′（x0+0）存在，则存在，且

即f′（x0+0）的存在性在某一条件下蕴涵了的存在.其详细的证明将在第十一课中给出.

下面给出两个例子说明在一般情况下二者不存在相互依存关系.

从上面的联系中，容易得到如下的结论：

设f（x）于x0点连续，于去心邻域U（x0，δ）内可导，如果(www.daowen.com)

则f（x）于x0点连续可导.

因此，该结果给出了另外一种判断函数是否可导的方法，但不是判断可导的充分必要条件，例如拓展习题讲解的例7.10.该方法对于在分段点的左右导数不容易计算时使用起来比较方便，例如课外练习的习题7.2和习题7.5.

7.2.2　拓展习题讲解

说明f（x）在点x0点右连续，同理，可以证明f（x）在点x0点左连续.

注　这个练习说明，只要左右导数存在，可以不相等，便蕴涵了连续，降低了课程中“可导必连续”这一命题的条件.另外，还可以看出，左导数存在蕴涵了左连续，右导数存在蕴涵了右连续.

解　在x≠0处可以用初等函数的求导法则，但是在点x=0处则必须按照导数的定义，先写出差商，再求极限.根据函数的定义，可以计算出f′（0）=0.从而得到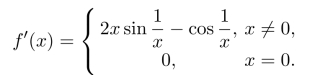

由此可见，函数f（x）处处可导，但是导函数f′（x）在点x=0处不连续.由于极限不存在，因此x=0为导函数f′（x）的第二类间断点.

注　函数f（x）在某一点x0可导，其导函数在该点不连续的例子不容易举出，本题正是提供了这样一个例子.

例7.11　设函数

讨论函数f（x）在（−∞，+∞）内的可导性.

解　先求极限得到函数的分段表达式，再对其分段点讨论可导性.

可以看出f（x）在区间（−∞，−1），（−1，1），（1，+∞）上可导.

所以x=1为不可导点.

例7.12　设函数f（x）在x0点可导，且f（x0）≠0，求证|f（x）|在x0点也可导.如果f（x0）=0，同样的结果还成立吗？

例7.13　设函数f（x）在x0点可导且f（x0）=0，则|f（x）|在x0点可导的充分必要条件是f′（x0）=0.

例7.14　设f（x）在x0点可导，则|f（x）|在x0点不可导的充分条件是（）.

（A）f（x0）=0且f′（x0）=0（B）f（x0）=0且f′（x0）≠0

（C）f（x0）＞0且f′（x0）＞0（D）f（x0）＜0且f′（x0）＜0

解　这三道题目实际上是一个问题，均基于如下的分析.

若f（x0）≠0，不妨设f（x0）＞0，由f（x）在x0点的连续性和保号性，可知存在x0的某个邻域O（x0，δ），当x∈O（x0，δ）时，f（x）＞0，因此

即|f（x）|在x0点可导.

若f（x0）=0，则

因此，在条件f（x0）=0下，|f（x）|在x0点可导的充要条件是f′（x0）=0.

从上面的分析过程可以看出，例7.14的答案为（B）.

注　这里用到了函数极限的性质，即如果则