5.2.1　基本习题讲解

例5.1　f（x）在x0点有定义，但是在这一点不连续的分析表述：

存在某个ε0＞0，对于任意的δ＞0，都存在一点xδ，满足|xδ−x0|＜δ，但是

例5.2　证明：若函数f（x）和函数g（x）都在区间（a，b）内连续，则函数φ（x）=min{f（x），g（x）}和ψ（x）=max{f（x），g（x）}也在（a，b）内连续.

证明　方法一，注意到

由f（x），g（x）的连续性，可得φ（x），ψ（x）在（a，b）内连续.

方法二，仅证明ψ（x）=max{f（x），g（x）}在（a，b）内连续.对于任意的x0∈（a，b），则f（x）和g（x）都在x0点连续，故对于任意的ε＞0，存在δ1＞0，当x∈O（x0，δ1）时，有

i）如果f（x0）＞g（x0），根据连续函数的“保号性”，则对于上述的ε＞0，存在一个邻域O（x0，δ2），当x∈O（x0，δ2）时，有f（x）＞g（x）.此时取δ=min（δ1，δ2），当x∈O（x0，δ）时，有

ii）如果f（x0）=g（x0），对于上述的ε＞0，此时取δ=δ1，当x∈O（x0，δ）时，有

iii）如果f（x0）＜g（x0），同i）可得到类似（5-5）式的结果.

再由x0的任意性，可得ψ（x）=max{f（x），g（x）}在（a，b）内连续.

例5.3　求下列函数的间断点，并指出间断点的类别.

解（1）当x≠0，x≠1时，函数有意义，且为初等函数，故为连续的.

当x=0时，函数无意义，且

所以为第二类间断点.

当x=1时，函数无意义，且

为第一类间断点.

（2）当x=0，x=1，x=−1三者之一时，函数没有意义，而在其他点是连续的.(www.daowen.com)

由于

故x=0为可去间断点.

5.2.2　拓展习题讲解

例5.6　若f（x0）在点x0连续，并且f（x0）＞0，证明：存在x0的邻域O（x0，δ），当x∈O（x0，δ）时，f（x）≥c＞0，c为某个常数.

注　这是连续函数的一个性质，即保号性.

证明f（x）在x0连续：对于任意ε＞0，存在δ＞0（δ与x0，ε有关），当|x−x0|＜δ时，有|f（x）−f（x0）|≤ε.

现取ε=f（x0）/2，则存在邻域δ′＞0（δ′依赖于x0，f（x0）/2），使得当|x−x0|＜δ′时，均有f（x）≥f（x0）−ε=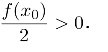

例5.7　说明y=Sgn（sinx）的连续性.

解　由画图形及简单计算，可知x=kπ（k=0，±1，±2，···）为其第一类间断点.

例5.8　假设对于所有x∈[−1，1]，均有|f（x）|≤|x|，证明f（x）在0点连续.

证明　易知f（0）=0，对于任意的ε＞0（不妨设ε＜1），取δ=ε，当|x−0|＜δ时，有|f（x）−f（0）|=|f（x）|≤|x|＜ε.

例5.9　设单调函数f（x）可以取到f（a）和f（b）之间的所有函数值，求证：f（x）在[a，b]上连续.

证明　假设f（x）在区间[a，b]上单调增加，对于x0∈（a，b），不妨设

则存在不同的两点x1∈（a，x0），x2∈（x0，b）使得

取δ=min{x2−x0，x0−x1}，则当|x−x0|＜δ时，由函数的单调性，知

得证.

对于其他如f（a）=f（b）、f（a）=f（x0）、f（b）=f（x0）等情形，可同理验证.