1.实数系的其他两个定理

（1）区间套定理

设闭区间列{[an，bn]}是一区间套，则存在唯一点ξ属于所有的闭区间[an，bn]，且

注意区间套的定义，一是闭区间列具有嵌套关系，二是区间长度趋于0，二者缺一不可.

例为一开区间列，不满足区间套定理.

例为一闭区间列，且具有嵌套关系，但其长度不趋于0，故也不满足区间套定理.

（2）致密性定理（仅作了解）

由第二课中知道，单调有界数列必收敛.仅仅有界的数列是否也收敛呢？答案是不一定.但是，有界数列{xn}必有收敛的子列，这一有关数列和子列的性质（第二课课外练习）就是致密性定理，可以用区间套定理证明之.

2.函数极限的定义

f（x）=A⇔设函数f（x）在x0的某一邻域内有定义（在x0点可以无定义），A是常数.对于任意的ε＞0，存在δ＞0，当0＜|x−x0|＜δ时，有

对于函数极限的分析定义的理解：

（1）δ不仅与ε有关系，还与函数f（x）在x0的邻域内的性态有关系，所以δ=δ（ε，x0），因此，函数的极限是一个局部性的概念.

（2）定义中的δ与数列的极限中的N的位置和作用相似.

（3）从函数的极限的定义可以看出，在点x0有无极限，与f（x）在x0处有无定义没有关系.

（4）f（x）在x0处没有极限的分析表述：

如果存在ε0＞0，对于任何δ＞0，总存在一点xδ，满足0＜|xδ−x0|＜δ，但是(www.daowen.com)

就称f（x）在点x0处不以A为极限.

如果f（x）在点x0处不以任何实数A为极限，则称f（x）在x0点没有极限.

3.函数的单侧极限的定义

=A⇔设函数f（x）在x0的右邻域内有定义（在x0点可以无定义），A是常数.对于任意的ε＞0，存在δ＞0，当0＜x−x0＜δ时，有

称A为f（x）于x0点的右极限，简记为

同理，可定义f（x）于x0点的左极限，并记为

由左、右极限的定义不难得到

由此，求分段函数（即函数在分段点两侧的表达式不一样）在分段点处的极限时，就可以利用左极限和右极限求之.例如

等.

注　函数的左、右极限有时也分别记为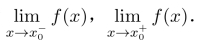

4.极限的复合计算.

定理3.1设

且在点x0的某个去心邻域内g（x）≠a，则

利用此结论可以证明一个幂指数函数求极限中的结果.