1.2.1　基本习题讲解

例1.1　证明：y=x−[x]为周期函数，并求出它的最小正周期.

证明[x]表示不超过x的最大整数.设周期为T，则：

可得到T为任意整数，故最小正周期为1.

所以就有

设xn=（−1）n，有

注　若a=0，二者是否等价呢？

1.2.2　拓展习题讲解

例1.3　给出函数f（x）在区间（a，b）内有界、数列{xn}有界的定义.

解f（x）在区间（a，b）内有界，即存在M＞0，使得对任意x∈（a，b）都有

|f(x)|≤M.

数列{xn}有界，即存在实数M＞0，对于任意的自然数n，均有

|xn|≤M.

例1.4　的定义与下面的叙述是否等价？

（1）∀ε＞0，∃N，当n＞N时，恒有|xn−a|＜ε.

解　是，由定义可以得到.

（2）∀ε＞0，∃N，当n＞N时，恒有|xn−a|＜Mε.（其中M是与ε无关的正数.）

解　是.(www.daowen.com)

（3）∀ε＞0，满足|xn−a|≥ε的n至多有有限多个.

解　是.

（4）∀ε＞0，满足|xn−a|＜ε的n有无限多个.

解　否.如数列x2n=1，满足条件，但是该数列发散.

（5）∃N，∀ε＞0，当n＞N时，恒有|xn−a|＜ε.

解　否，是的充分条件，但非必要条件.

（6）任意的正整数m，存在N，∀n＞N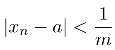，均成立.

解　是.

（7）∀0＜ε＜10−10，∃N，当n＞N时，恒有|xn−a|＜ε.

解　是.

得证.

注　方法一的证明不同于教材上的方法.

注　是否有类似于例1.6题的方法来证明此题？答案是肯定的，注意到

成立.

令N=max{N1，N2}，当n＞N时就有

注　结论（1-3）也称为施笃兹（Stolz）定理.详细的内容见参考文献[1]，在证明数列的极限时可以直接应用.