1.物料平衡 在任一化学工艺过程中,都必须对给料总量与最终产品量进行比较并作出分析,这种比较与分析称为物料平衡。
化学方程式是使用符号和分子式简捷地表述化学变化和物料平衡。书写化学方程式要注意以下几点:
(1)必须是实际发生的反应。
(2)要“配平”化学方程式,使反应物和生成物中同种元素的原子总数相等,符合质量守恒定律。
(3)当反应必须在一定条件下才发生时,要在“=”或“→”符号的上下位置注明反应条件。
(4)生成物是沉淀物时加注“↓”,是气体时加注“↑”。
例如,甲烷与氧反应(燃烧)生成二氧化碳和水,这个反应的未平衡化学方程式是:CH4(气)+O2(气)→CO2(气)+H2O(液)+能量
参与反应的物质叫反应物,写在箭头的左侧,反应生成的物质叫生成物,写在箭头的右侧,箭头表示反应的方向,意为“生成”,加号“+”意为与,符号“气”表示气体,符号“液”表示液体,符号“水”表示水溶液,即溶解于水的物质。
(1)方程式中的分子关系。化学方程式必须满足两个条件:实验的事实及质量守恒定律。第一个条件就是化学方程式要写出参与反应的所有反应物和生成物,并使用正确的符号和分子式表示这些物质;第二个条件则必须是每种生成物原子都具有与反应物原子相同的数目,这是因为质量守恒定律认定,在化学反应中质量没有损失。
例如:C(固)+O2(气)→CO2(气)
反应物有一个碳原子和两个氧原子,生成物也有一个碳原子和两个氧原子,故上述方程是平衡的。如果一个方程式不平衡,则要进行配平,就是在适当的符号或分子前加系数,使它达到平衡。
例如:CH4(气)+O2(气)→CO2(气)+H2O(液)+能量
反应物有4个氢原子和两个氧原子,生成物有两个氢原子和三个氧原子,这是不平衡的,需要在反应物O2前加系数“2”,生成物H2O前加系数“2”,即原方程式变为
CH4(气)+2O2(气)=CO2(气)+2H2O(液)+能量
这就达到了平衡。不能用改变反应物或生成物分子式的方式来求得方程式的平衡。
例如,水的分子式是H2O,而不是H2O2,如改为H2O2虽能使方程式平衡,但它不代表实验事实。下面举两个例子,说明化学方程式的配平。
例1:氨(NH3)在氧气(O2)中燃料产生(N2)和水(H2O),试写出该反应的化学方程式
解:NH3+O2→N2+H2O
左边1个N、3个H、2个O,右边2个N、2个H、1个O,配平后即为
4NH3+3O2=2N2+6H2O
分子式前的系数,可反复试配。
例2:试计算下列化学方程式中反应物和生成物含有的原子数目。
4NH3+3O2=2N2+6H2O
反应物:4×1N=4N
4×3H=12H
3×2O=6O
生成物:2×2N=4N
6×2H=12H
6×1O=6O
(2)方程式中的质量关系。将分子式中每个原子的原子质量相加即可求得分子质量。使用周期表,周期表已标明了每个原子的相对原子质量,把分子中所有原子的相对原子质量加起来,就能计算出任何化合物的相对分子质量(分子量)。
例1:计算化学方程式H3PO4+3KOH=K3PO4+3H2O中各分子的相对分子质量。
解:①计算H3PO4的相对分子质量:
3H=3×1.008=3.024
1P=1×30.98=30.98
4O=4×16.00=64.00
H3PO4的相对分子质量=98
②计算KOH的相对分子质量:
3K=3×39.1=39.1
1O=1×16.00=16.00
1H=1×1.008=1.008
KOH的相对分子质量=56
③计算K3PO4的相对分子质量:
3K=3×39.1=117.3
1P=1×30.98=30.98
4O=4×16.00=64.00
K3PO4的相对分子质量=212
④计算H2O的相对分子质量:
2H=2×1.008=2.016
1O=1×16.00=16.00
H2O的相对分子质量=18
⑤反应物和生成物的总相对分子质量分别为:
98H3PO4+16KOH=266
212K3PO4+54H2O=266
这就是所谓的质量守恒,在正常的化学反应中,反应物的质量等于生成物的质量,质量既不能被创造,也不能被消灭。由于原子质量是相对质量,所以相同的质量守恒关系可适用任何其他单位。
(3)比例因子法。用比例因子法可以方便地计算所需的生成物。
例:试计算与36.0g碳完全化合所需的氧气量。
解:已知12gC+32gO2=44gCO2
从上式知,12gC需要32gO2,用比例因子法可得:
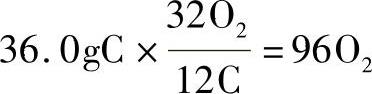
因此所需的氧气为92g。
(4)摩尔单位。对于系数不是1∶1的化学反应,采用摩尔(mol)为单位进行计算非常方便。在化学工艺过程中以一个原子或分子为单位进行化学计算,则显得毫无意义,以至于无法处理,因此采用摩尔作为计量单位。
以质量表示:一个摩尔定义为一个元素的原子质量或一个化合物的分子质量。
以粒子、原子或分子的数目表示:一个摩尔定义为6.02×1023,称为阿伏加德罗数,对化学计算非常重要。
例:当1000g甲烷燃料与氧气反应时,会生成多少克的水?
解:燃烧化学方程式如下:
CH4+2O2=CO2+2H2O
①1mol甲烷(CH4)分子质量为
(1×12.0g)+(4×1.01g)=16.0g
②1000g甲烷的摩尔数为:
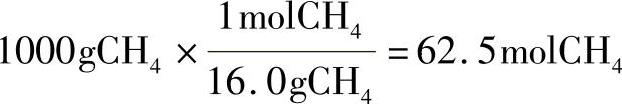
③1000g甲烷生成的水的摩尔数为:
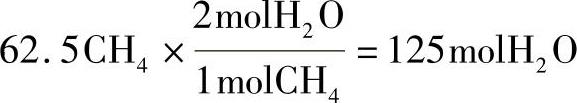
④将水转换成以克为单位表示:
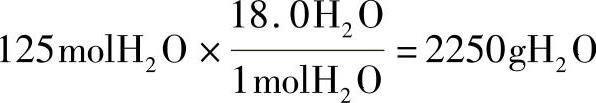
1000g甲烷燃料时,会生成2250g的水。
由上例可以看出,一个平衡的化学方程式,其化学式前面的数字系数代表着反应中每种参与反应或反应生成的物质的摩尔数。
2.生成率 上述计算反应假定都是完全的,即所有反应物全部耗尽,而生成物的生成量最大。换言之,计算的是理论生成量。事实上,纯态物质的实际生成量都小于理论生成量,某些生成物往往在分离和提纯工艺过程中损失,我们用生成率来表示生成物的损失。

3.浓度 浓度是溶质在一已知数量的溶剂或溶液中的数量。
(1)溶液表示两种或两种以上物质的均匀混合物,溶液由两部分组成,主要部分称为溶剂,是一种溶解物质,而次要部分为溶质,它是一种或多种被溶解物质,溶质+溶剂=溶液。最常见的溶液的溶剂为水,而溶质为可溶固体、可溶气体或可混溶液体的溶液。
例如:固体/液体→糖溶于水
气体/液体→二氧化碳溶于水
液体/液体→乙醇溶于水
固体/固体→黄铜是锌溶于铜
气体/气体→空气是氧和其他气体溶于氮中
(2)可混溶。液体溶质可全部溶解于液体溶剂中,形成各种配比。
(3)不混溶。形成两层,完全不相溶解,如油和水。
(4)固体溶质溶解于液体溶剂取决于若干因素,如温度影响溶解过程的速率和程度。
(5)浓度三种表示方式,即百分率,百万分率(ppm)、十亿分率(ppb),摩尔浓度。
1)百分率是指溶质在总溶液中所占的百分数。
①以质量为量度的百分率[%(wt/wt)]
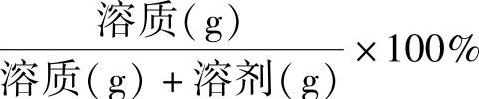
②溶质以质量量度,溶剂以容积量度的百分率[%(wt/V)]
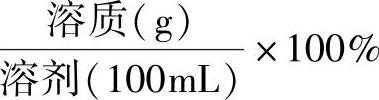
③以容积为量度的百分率[%(V/V)]

例:用100mL丙酮溶于1.0L的纯水中制备一种溶液,丙酮的密度为0.79g/mL,水的密度为1.00g/mL,试计算%(wt/wt)、%(wt/V)、%(V/V)。
解:丙酮的质量为:100mL×0.79g/mL=79.0g
水的质量为:1.0L=1000mL×1.00g/mL=1000g
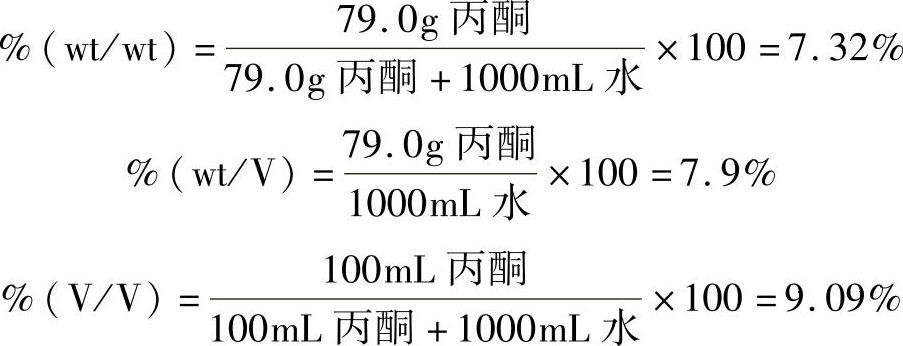
2)百万分率(ppm)是指每百万份溶液中有一份溶质的溶液浓度。

十亿分率(ppb)是指每十亿份溶液中有一份溶质的溶液浓度。

例:用10.0mL乙二醇在1.00L水(密度=1.00g/mL)中稀释成乙二醇溶液,其浓度为多少ppm(wt/wt)?(乙二醇密度=1.11g/mL)(https://www.daowen.com)
解:①计算10.0mL乙二醇的克数。
10.0mL乙二醇×1.11g/mL=11.1g乙二醇
②计算1.00L水的克数。
1.00L水=1000mL水×1.00g/mL=1000g水
③计算ppm(wt/wt)。
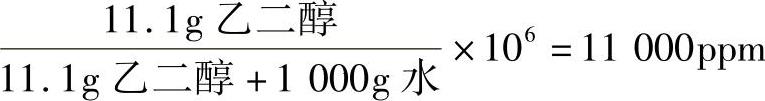
3)摩尔浓度。摩尔浓度(M)也叫克分子浓度,定义为每升溶液的溶质摩尔数,任何一摩尔物质的质量等于它的相对分子量。多数情况下,相对分子量可以直接从生产商的说明书或化工手册中查得。

例1:如果265g氟化钠(NaF)溶解于足量的脱离子水中生成355mL溶液,该溶液的摩尔浓度是多少?
解:氟化钠的相对分子量=41.988g/mol。
①将NaF的克数转换成摩尔数:
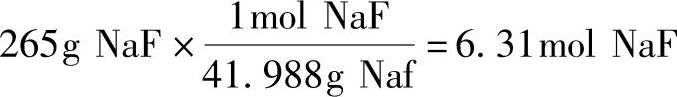
②将容积从mL转换成L:
355mL=0.355L
③计算溶液的摩尔浓度:
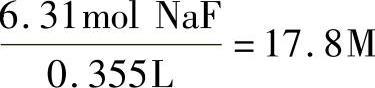
例2:如果200mL丙酮溶解于足量的水中制成8.00L的溶液,则摩尔浓度是多少?丙酮密度为0.79g/mL,相对分子质量为58.08g/mol。解: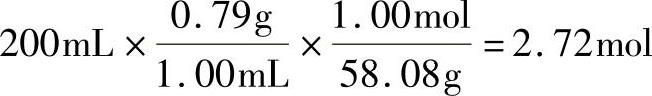
丙酮摩尔浓度=2.72moL/8.00L溶液=0.34M
4.氧化还原反应 在反应中有电子转移的反应称为氧化还原反应。
Zn+Cu2+→Zn2++Cu
失去电子的物质(Zn)叫做还原剂,得到电子的物质(Cu2+)叫做氧化剂。氧化剂从还原剂获得电子,使自身的化合价降低,这个过程叫做还原。相应地还原剂由于给予电子,而使自身的化合价升高,这个过程叫做氧化。在氧化还原反应中,氧化与还原是共存共依的,在一定条件下又可以相互转化。
5.稀释 为减少货运成本,经常采购浓缩的化学品,使用时再加以稀释。适用于任何浓度单位的稀释公式如下:
C0V0=CfVf
式中 C0——库存溶液的原始浓度;
V0——待稀释的库存溶液容积;
Cf——最终(稀释后的)溶液浓度;
Vf——最终(稀释后的)溶液容积。
例:一个操作人员应用多少12.0M的HCl浓缩液制备成75.0gal 2.50M的HCl溶液?
解:由C0V0=CfVf可得:
12.0M HCl×V0=2.50M HCl×75.0gal
V0=15.6gal
所需水量=75.0gal-15.6gal=59.4gal
操作人员应用15.6gal 12.0M的HCl浓缩液稀释成总容积为75.0gal的溶液,才能制成所要求浓度的2.50M HCl溶液。
6.酸 酸是一种溶于水时生成氢离子(H+)的物质,水溶液味酸。酸能使石蕊试纸变红,与活性金属如锌和铁反应,使金属溶解并生成氢气。
在水溶液中酸的性质则归因于水合的氢离子,即一个氢离子至少附着一个水分子。常见酸的电离反应如下:
HCl→H+(水)+Cl-(水)
HNO3→H+(水)+NO3-(水)
酸分强酸和弱酸,强酸在水中几乎百分之百离子化,即几乎所有的酸分子都分离为离子。常见的强酸有硫酸、盐酸、硝酸等。弱酸在水溶液中仅轻度离子化,多数呈分子状态,一般只有5%的酸分子以H+离子形式存在。
7.碱 是一种溶于水时生成氢氧离子(OH-)的物质,水溶液味苦,能使石蕊试纸变蓝。常见碱的电离反应如下:
NaOH→Na+(水)+OH-(水)
Mg(OH)3→Mg2+(水)+2OH-(水)
8.pH标度pH值是氢离子摩尔浓度[H+]的简单数学记数制表达,它避免了使用指数记数制的表达。氢离子浓度在25℃时的mol/L数如表8-2所示。该标度上1×10-7M的氢离子浓度对应为pH值7,1×10-10M的氢离子浓度对应为pH值10等,按定义,pH值等于以mol/L表示的氢离子浓度的负对数:
pH=-log[H+]
表8-2 氢离子浓度在25℃时的mol/L数
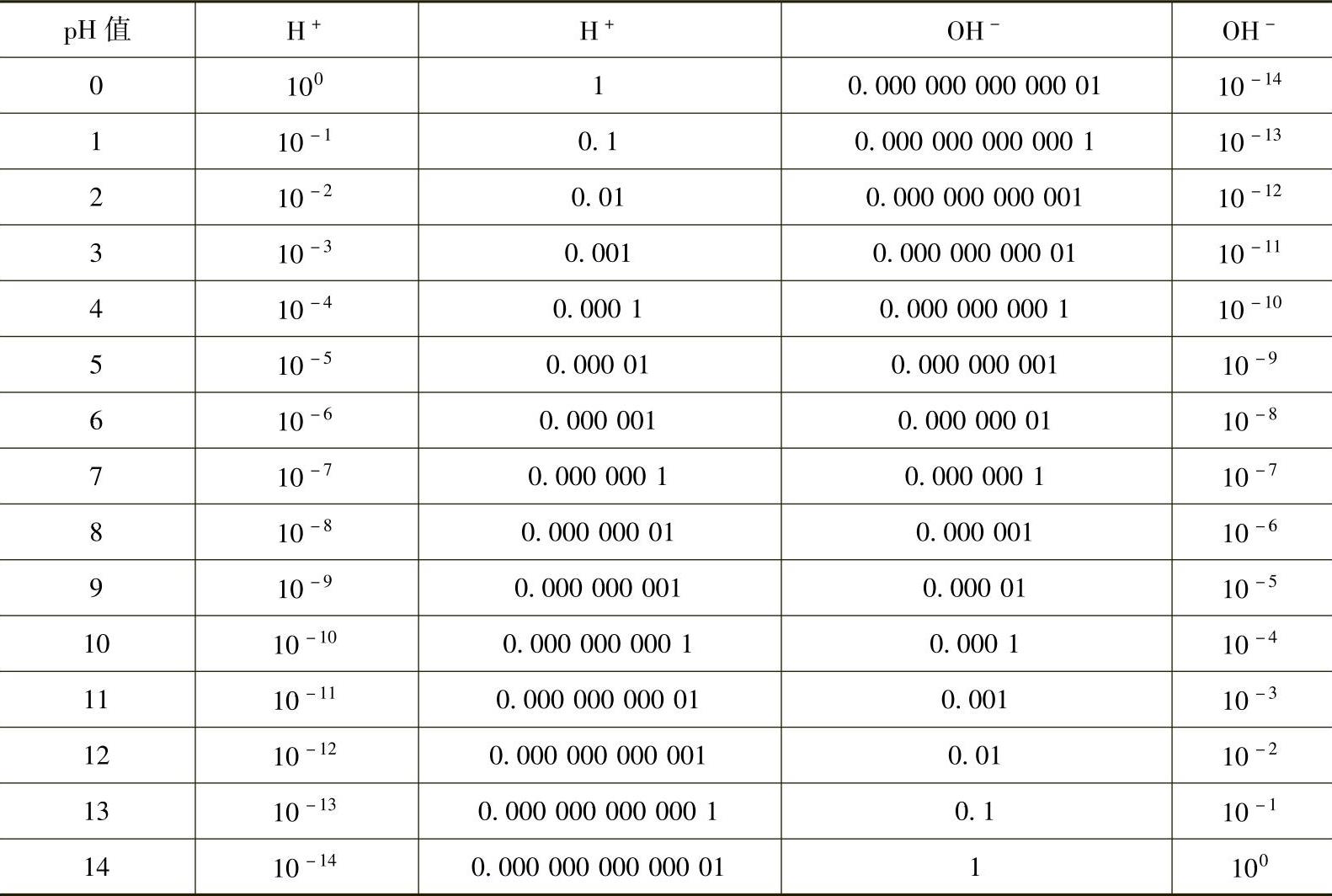
如果pH值等于7,溶液呈中性;如果pH值小于7,溶液呈酸性;如果pH值大于7,溶液呈碱性。pH值通常用指示剂或pH计测定,指示剂随pH值变化而改变颜色。加少量指示剂于溶液中,并观察其颜色,就能够确定pH值。pH计是一种电子设备,可以直接显示pH值。也可以用pH试纸来测定pH值。
9.中和 中和是指酸与碱接触生成盐与水的反应。
酸+碱→盐+水
如:HNO3+NaOH=NaNO3+H2O
酸的氢离子(H+)与碱的氢氧根离子(OH-)反应生成水。如果碱中有两个氢氧根离子,就需要两个氢离子使它们完全中和:
2HCl+Ca(OH)2=CaCl2+2H2O
10.滴定 滴定是一种分析方法,用一种已知浓度的溶液与一种未知浓度的溶液反应,以求得未知溶液的浓度,常用下式确定(仅适用于生成等量H+离子和OH-离子的酸/碱中和反应):
CAVA=CBVB
式中 CA——酸的浓度;
VA——酸的容积;
CB——碱的浓度;
VB———碱的容积。
例:如果需要27.77mL HCl去中和45.44mL 0.2233M NaOH溶液,试计算盐酸溶液的浓度。
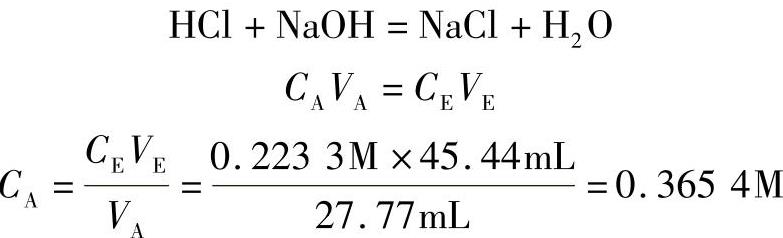
11.压力 压力常用的单位及换算方式如下:
psi 磅力每平方英寸 lbf/in2
Pa 帕,牛顿每平方米 N/m2
atm 大气压
bar 巴
1atm=14.696lbf/in2(psi)
=29.921inHg
=76cmHg
=760mmHg(广泛使用的定义)
=760Torr
=33.899ftH2O
=10.33mH2O
=1.01325×105Pa
=101.325kPa(广泛使用的定义)
=1.01325×106dyn/cm2
1bar=1×105Pa(帕斯卡)=0.1MPa
英制转换公式:
gal×3.785=liters
lb×0.454=kg
psi×6.7=kPa
(°F-32)/1.8=℃
12.数字的归组 在SI(国际单位制)中,不推荐用逗号隔开1000的倍数,而用空格代替逗号,小于1的数必须在小数前加零。
例如:34,908,788,762,433=34908788762433
.3456=0.3456
13.工程记数显示 以指数增量3表示的数。
例如:定位计数:0.0166666667
科学记数:1.666666-02
工程记数:16.66666-03
14.科学计数器
(1)定位记数显示,如果数字超出所选择的位数,自动地圆整显示最末位的有效数字。
(2)用指数记数制表示数:由两部分组成,一部分显示数,即数字部分,另一部分是10的若干方次,如5678表示成5.678×103。
15.SI单位制 国际单位制,也称为公制系统,有七个基本单位。SI制的基本单位如表8-3所示。
表8-3 SI制的基本单位

注:()内的字,是在不致混淆的情况下,可以省略的字。
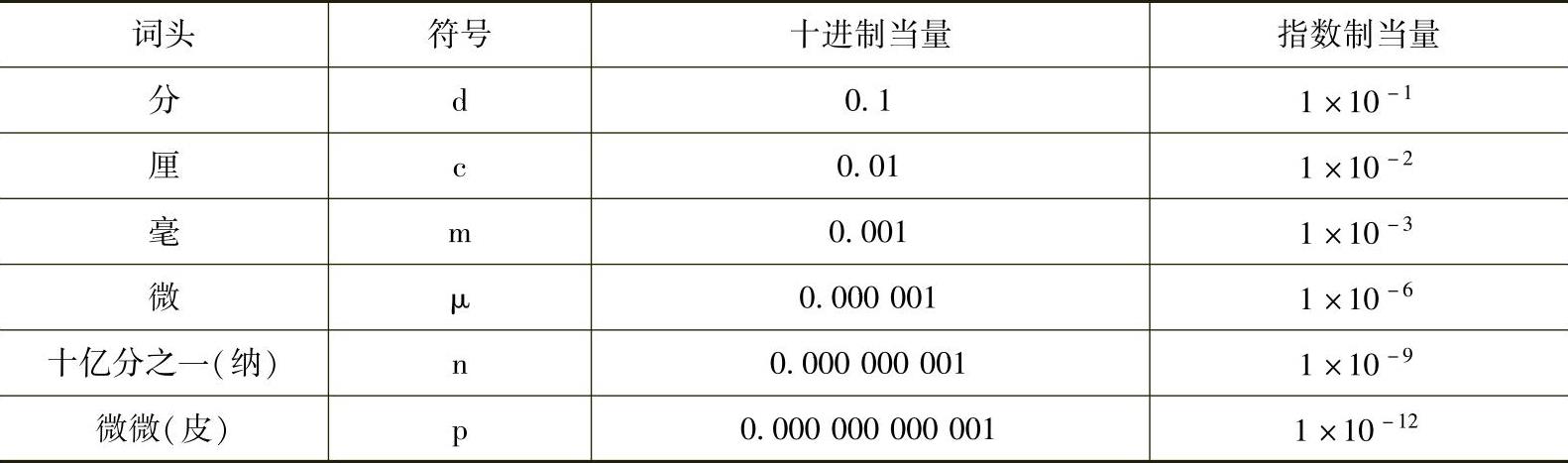
16.SI制的词头系统SI制的词头系统如表8-4所示。
表8-4 SI制的词头系统
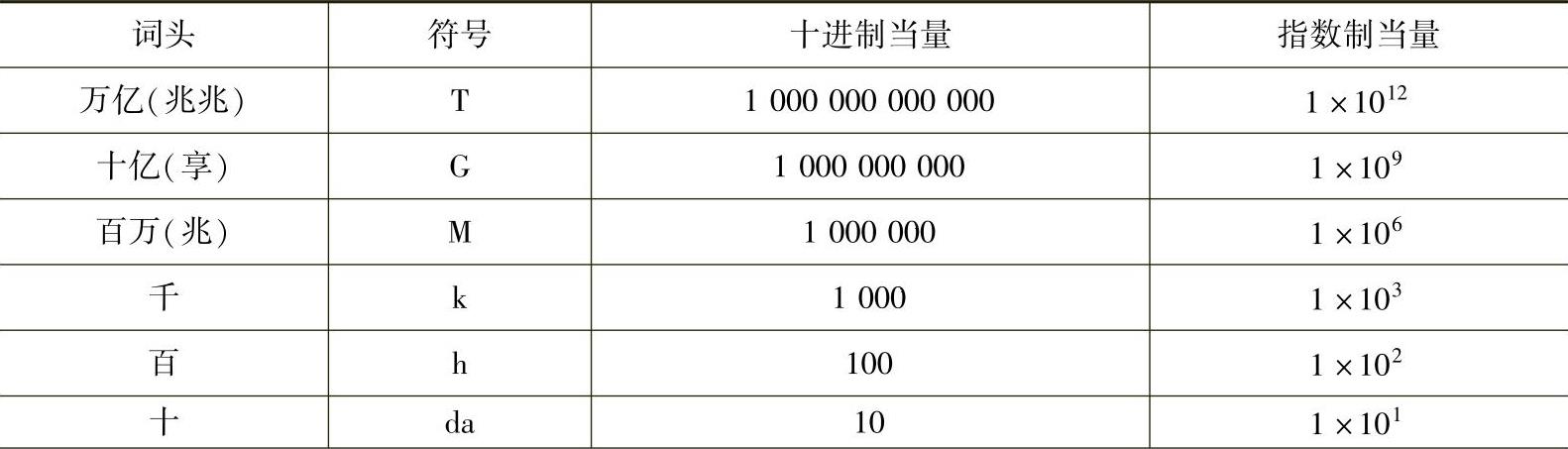
(续)
17.粒度的分级
10目——每平方英寸10×10个孔。
200目——每平方英寸200×200个孔。
20/60——物料能通过20目的筛子,但不能通过60目的筛子。
筛分:将试样放在叫做套筛的一连串筛子上,套筛作回转运动,并不时以撞击的方式振动试样平台,支持着筛子作回转运动,顶部锤子提供规则的轻敲动作,颗粒从顶部最粗的筛网缓慢落下至底部最细的筛网上,比网眼大的颗粒保留在该筛网上。这种方法可得到一系列的截留物,对每层一截留物进行称重,即可求得每个筛上截留物的质量百分比。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








