Hough变换的基本思想是利用点—线的对偶性。它可以将笛卡儿坐标空间的线变换为极坐标空间中的点。图8(a)是笛卡儿坐标中的一条直线，如果用ρ代表直线距原点的法线距离，θ为该法线与x轴的夹角，则可用如下参数方程来表示该直线。这一直线的Hough变换为：

ρ=x cosθ+y sinθ

在极坐标中便是图8(b)所示的点(ρ，θ)，在极坐标里，横坐标为直线的法向角θ，纵坐标为笛卡儿坐标原点到直线的法向距离ρ。在笛卡儿坐标系中通过公共点的一簇直线[图8(c)]，映射到极坐标中便是一个点集，这些点集构成一条曲线，其实这正好是正弦曲线[图8(d)]。因此笛卡儿坐标空间中的一个点对应于极坐标中就是一条正弦曲线。

在笛卡儿坐标中共直线的点[如图8(e)中的(x 1，y 1)，(x 2，y 2)，(x 3，y 3)三点共线]映射到极坐标系便是共点的一簇曲线[图8(f)]。在图8(f)中还可以看到这三条曲线有两个交点，其实这两个交点的所对应的横坐标值即法向角数值相差180°，对应到笛卡儿坐标里是同一条直线。如果令直线的法向角的取值范围为：0≤θ≤π，其交点就只有一个了。从图8中可以看出，Hough变换使不同的线和点建立了一种对应关系。(www.daowen.com)

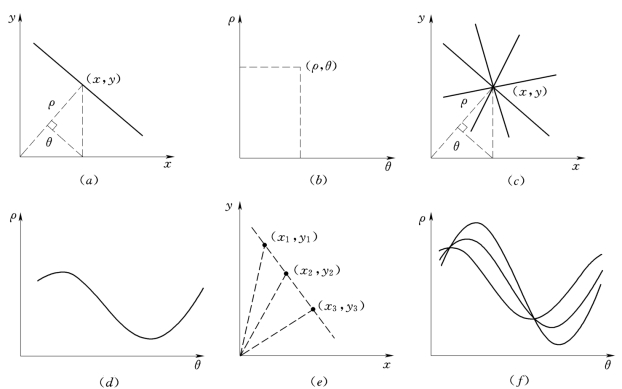
图8　Hough变换