一、矢量和标量

物理学中我们经常会遇到两类物理量：一类物理量，如时间、质量、能量、温度等，只有大小和正负，而没有方向，这类物理量称为标量；另一类物理量，如位移、速度、力、动量等，既有大小又有方向，而且合成时遵从平行四边形运算法则，这类物理量称为矢量。

矢量通常用黑体字母A来表示，作图时，常用有向线段（图A-1）来表示，线段的长度按一定比例表示矢量的大小，箭头的方向指向矢量的方向。

矢量的大小叫做矢量的模，矢量A的模常用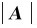或A表示。如果矢量e_A的模等于1，且e_A方向与矢量A相同，则称e_A为矢量A方向上的单位矢量。引进单位矢量后，矢量A可表示为

如把矢量在空间平移，矢量的大小和方向都不会改变，矢量的这一性质称为矢量的平移不变性，它是矢量的一个重要性质。

二、矢量合成的几何法

1.矢量相加

利用平行四边形求合矢量的方法叫做矢量相加的平行四边形法则。如图A-2所示，设有两个矢量A和B，将它们相加时，可将两矢量的起点交于一点，以这两个矢量为邻作平行四边形，从两矢量的交点作平行四边形的对角线，此对角线即代表A和B两矢量的和。用矢量式表示为

C=A+B

C称为合矢量，而A和B则称为矢量C的分矢量。

显然，矢量合成的平行四边形法则也可简化为三角形法则，即将矢量A和B首尾相连，由A的起点至B的末端的矢量就是合矢量A+B，如图A-3所示。并且，连续使用三角形法则，则可得到多个矢量相加的多边形法则，即把多个矢量首尾相接，从第一个矢量的起点至最后一个矢量的末端的直线矢量就是它们的矢量和（图A-4）。

合矢量的大小和方向可通过计算求得。如图A-5所示，合矢量C的大小和方向很容易求得

2.矢量相减

两矢量A与B之差也是一个矢量，用A-B表示。矢量A与B之差可写成矢量A与矢量-B之和，即

A-B=A+（-B）

如同两矢量相加一样，两矢量相减也可以采用平行四边形法则[图A-6（a）]。从图A-6（b）也可以看出，如两矢量A和B从同一点画起，则自B末端向A末端作一矢量，就是A与B之差A-B。

求矢量差的大小和方向，仍可用式（A-1）、（A-2）进行计算，但必须注意，这时角α是A和-B之间小于π的夹角。

三、矢量合成的解析法

1.矢量在直角坐标轴上的分矢量和分量

由前述已知，任意几个矢量可以相加为一个合矢量。反过来，一个矢量也可以分解为任意数目的分矢量。就一个矢量分解为两个分矢量而言，相当于已知一平行四边形的对角线求平行四边形两邻边的问题（图A-7）。由于对角线不变的平行四边形可以有无限多种，因此把一个矢量分解为两个分矢量可以有无限多种方法，但可以根据一定的条件作出确定的分解。如已知两分矢量的方向；或已知一个分矢量的大小和方向；或已知两分矢量的大小等。

在实际问题中，常把一个矢量在选定的直角坐标系上进行分解。如图A-8所示，在平面坐标系Oxy上，矢量A的始端位于原点O，它与x轴的夹角为α。从图可见，矢量A在x轴上的分矢量A_x和在y轴上的分矢量A_y都是一定的，即

A=A_x+A_y

若沿Ox轴的正向取一长度为1的单位矢量i，沿Oy轴的正向取一长度为1的单位矢量j，则两分矢量A_x和A_y为

A_x=A_xi A_y=A_yj

其中，A_x和A_y分别是矢量A在x轴和y轴上的分量的值，即它们是矢量A_x和A_y的模，所以有

A_x=Acosα A_y=Asinα

应当注意，角α是由Ox轴按逆时针方向旋转至A的角度。于是式（A-3）可写成

A=A_xi+A_yj

显然，矢量A的模为

矢量A与x轴的夹角α以及分量A_x、A_y之间的关系为

分量A_x、A_y的值可正可负，取决于矢量A与x轴的夹角α。由式（A-4）可见，当A与x轴的夹角α=0时，A_x=A, A_y=0；当α=π时，A_x=-A, A_y=0。

若一矢量A在如图A-9所示的三维直角坐标系中，那么它在x、y和z轴上的分矢量分别为A_x、A_y和A_z，于是有

A=A_x+A_y+A_z

另外，矢量A在x、y和z轴上的分量分别为A_x、A_y和A_z。如以i、j和k分别表示x、y和z轴上的单位矢量，则有

A=A_xi+A_yj+A_zk

矢量A的模为

矢量A的方向由该矢量与x、y和z轴的夹角α、β和γ来确定，有

2.矢量合成的解析法

运用矢量在直角坐标轴上的分量表示法，可以使矢量加减运算简化。设平面直角坐标内有矢量A和B，它们与x轴的夹角分别为α和β（图A-10）。根据式（A-4），矢量A和B在两坐标轴上的分量可表示为

由图A-10可以看出，合矢量C在两坐标轴的分量Cx和Cy与矢量A、B的分量之间的关系为

式（A-7）亦可用式（A-3）导出。因为

A=A_xi+A_yj, B=B_xi+B_yj

所以

C=A+B=（A_x+B_x）i+（A_y+B_y）j

而

C=C_xi+C_yj

故亦有

矢量C的大小和方向由下列两式确定：

四、矢量的标积和矢积

在物理学中，除经常遇到相同矢量的加减外，还经常遇到不同矢量的乘积。矢量乘积常见的有两种：一种是标积（或称点积、点乘），一种是矢积（或称叉积、叉乘）。例如，功是力和位移两矢量的标积，力矩是位矢和力两矢量的矢积。

1.矢量的标积

设两矢量A和B之间的夹角为α，矢量A和B的标积用符号A·B表示，并定义

A·B=ABcosα

即矢量A和B的标积是矢量A和B的大小及它们夹角α余弦的乘积，为一标量。由图A-11可见，A·B也相当于A的大小与B沿A方向分量的乘积（或相当于B的大小与A沿B方向分量的乘积）。当A与B同向时（α=0°），A·B=AB；当A与B反向时（α=180°），A·B=-AB；当A与B互相垂直时（α=90°），A·B=0。

从标积的定义可以得到标积的如下性质：

（1）标积遵守交换律，即

A·B=ABcosα=BAcosα=B·A

（2）标积遵守分配率，即

（A+B）·C=A·C+B·C

在直角坐标系中，有两矢量A和B，它们分别为

A=A_xi+A_yj+A_zk

B=B_xi+B_yj+B_zk

于是它们的标积为A·B=（A_xi+A_yj+A_zk）·（B_xi+B_yj+B_zk）=A_xB_xi·i+A_yB_yj·j+A_zB_zk·k+A_xB_yi·j+A_xB_zi·k+A_yB_xj·i+A_yB_zj·k+A_zB_xk·i+A_zB_yk·j

利用上述标积的性质，可得

i·i=j·j=k·k=1

i·j=j·i=i·k=k·i=k·j=j·k=0(www.daowen.com)

于是，上式为

A·B=A_xB_x+A_yB_y+A_zB_z

2.矢量的矢积

设两矢量A和B之间小于180°的夹角为α。A和B的矢积用符号A×B表示，并定义它为另一矢量C，即

C=A×B

矢量C的大小为

C=ABsinα

矢量C的方向垂直于A和B所在的平面，其指向可用右手螺旋法则确定。如图A-12所示，当右手四指从A经小于180°的角转向B时，右手拇指的指向（右螺旋前进的方向）就是C的方向。如果以A和B构成平行四边形的邻边，则C是这样的一个矢量，它垂直于四边形所在的平面，且其指向代表着此平面的正法线方向；而它的大小则等于平行四边形的面积。

利用矢积的定义，可以得到矢积具有如下性质：

（1）矢积不遵守交换定律。由于A×B的大小ABsinα与B×A的大小BAsinα相同，但A×B和B×A的方向相反，所以

A×B=-B×A

（2）如果矢量A和B是平行或反平行，即它们之间的夹角α为0或180°时，由于sinα=0，所以B×A=0

（3）矢积遵守分配率，即

C×（A+B）=C×A+C×B

利用i×j=k, i×k=-j, i×i=0，以及相应的项，可得

A×B=（A_xi+A_yj+A_zk）×（B_xi+B_yj+B_zk）=（A_yB_z-A_zB_y）i+（A_zB_x-A_xB_z）j+（A_xB_y-A_yB_x）k

上式还可写成行列式

五、矢量的导数和积分

1.矢量的导数

如图A-13所示，在直角坐标系中有一矢量A，它仅是时间的函数。随着时间的流逝，矢量A的大小和方向都在改变。设在时刻t，该矢量为A₁（t），在时刻t+Δt，这矢量为A₂（t+Δt）。那么在Δt时间间隔内，其增量为

ΔA=A₂（t+Δt）-A₁（t）

当Δt→0时，

的极限值为

式中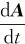，为矢量A对时间t的导数。在一般情况下，矢量A不仅是时间t的函数，还可以是坐标x、y、z等的函数，即是多元函数。关于多元函数的求导，请参阅有关数学书籍。

矢量函数的导数常用其分量函数的导数来表示。在直角坐标系上，矢量A从A₁改变为A₂，A₁和A₂可分别写成

A₁=A_1xi+A_1yj+A_1zk

A₂=A_2xi+A_2yj+A_2zk

于是A的增量

ΔA=（A_2x-A_1x）i+（A_2y-A_1y）j+（A_2z-A_1z）k

如令

ΔA_x=A_2x-A_1x，ΔAy=A_2y-A_1y，ΔA_z=A_2z-A_1z

则有

ΔA=ΔA_xi+ΔA_yj+ΔA_zk

把上式代入式（A-18），可得

即

利用矢量导数的公式可以证明下列公式：

（1）

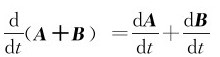
（2）

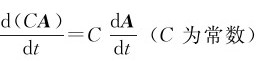
（3）

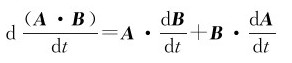
（4）

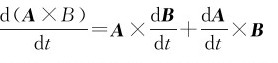
矢量导数在物理学中是很有用的。读者可以参阅第1章关于瞬时速度和加速度的定义。

2.矢量的积分

矢量函数的积分是很复杂的。下面举两个简单的例子。

设A和B均在同一平面坐标系内，且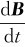=A。于是，有

dB=Adt

对上式积分并略去积分常数，得

B=∫Adt=∫（A_xi+A_yj）dt

即

B=（∫A_xdt）i+（∫A_ydt）j

其中

B_x=∫A_xdt, B_y=∫A_ydt

式（A-20）在物理学中是经常遇到的，如计算直线运动和曲线运动的位置矢量或位移，以及力的冲量等。

若矢量A沿如图A-14所示的曲线变化，那么

∫A·ds

是这个矢量沿此曲线的线积分。由于

A=A_xi+A_yj+A_zk

ds=d_xi+d_yj+d_zk

所以

∫A·ds=∫（A_xi+A_yj+A_zk）·（d_xi+d_yj+d_zk）

由于

i·i=j·j=k·k=1

i·j=j·i=i·k=k·i=k·j=j·k=0

可得

∫A·ds=∫A_xdx+∫A_ydy+∫A_zdz

若上式中的A为力，ds为元位移，则式（A-21）就是变力做功的计算式。