§14-5　微观客体的状态描述

在经典力学中，粒子在某一时刻的状态可以用坐标r和动量p（更一般的为广义坐标和广义动量）这一对物理量完全确定。粒子随时间的变化规律由运动方程给出。理论上，只要知道某一时刻粒子的位置、动量和力场的性质，就可从牛顿运动方程预言粒子以后的行为。粒子在运动历程中，总是描绘出一条确定的轨迹，粒子运动遵从决定性的规律。微观粒子具有波粒二象性，其运动状态的描述以及状态随时间的变化规律，当然不可能搬用经典力学的方法。

一、不确定关系

设一束具有确定动量p的电子投射到宽度为d的狭缝上，电子投射方向垂直缝的平面，令x轴平行于缝平面，y轴垂直于缝平面，如图14-11所示。

根据德布罗意的理论，电子单缝衍射与光的单缝衍射在物理本质上是相同的。实验表明，其衍射图样完全一致。所以，电子的物质波波长、半角宽度α满足关系：

当电子经过狭缝的时刻，它的坐标x被确定到精确度Δx=d，由于电子具有波动性，它通过狭缝产生衍射，导致在x方向的分散，即电子动量的x分量p_x发生了变化（进入狭缝前p_x=0），而且变化不是一个确立值，具有一定的分布。因为衍射图样的强度主要集中在中央极大，则电子在x方向的分布主要集中在第一级极小之间，故p_x的不确定度Δp_x为

即有

Δx·Δp_x≥h

式（14-23）称为海森伯不确定关系。它可以被表述为：粒子在某方向坐标的不确定量和该方向上动量分量的不确定量的乘积，一定不小于普朗克常数。

不确定关系表明，Δx和Δp_x不能同时为零，也不能同时无限地减小。因此，x、p_x（同样y和p_y，z和p_z）不能同时有确定值。亦即，不可能同时准确地测量一个粒子在某一方向上的位置和动量值。粒子的坐标和动量的这种不确定关系，既不是由于测量仪器的精度不够，也不是测量方法引起的某种误差。试图使用更精密的仪器和改善测量技术来消除这种不确定性，都将于事无补。不确定关系是由物质的固有属性决定的，是波粒二象性的反映，是波粒二象性原理性的表述。它给出了经典力学量的概念在微观粒子上的适用程度。不确定关系是微观领域中一条基本规律。

由式（14-23）看出，不确定关系Δx·Δp_x≥h, h的量纲是J·s。我们把相乘以后量纲为J·s的两个物理量，称作共轭物理量。显然，坐标和动量（r, p），角动量和角位移（L，φ）都是一对互为共轭的物理量。将海森伯不确定关系推广到一对互为共轭的物理量，其表述为：互为共轭的一对物理量，其不确定度的乘积，绝不小于普朗克常数。例如，能量和时间乘积的量纲为J·s，它们的同时测量存在不确定关系

ΔE·Δt≥h

其中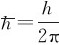，，ΔE和Δt分别表示能量和时间的不确定度。当原子处于某激发态时，并不是稳定的，将有一定的概率自发地跃迁到低激发态或基态，即原子处于每一激发态都有一定的寿命；另外，每一激发态能量取值有一定的范围，称为能级宽度。能级宽度ΔE和该能级的平均寿命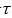满足下式：

由于能级有一定的宽度，原子光谱的谱线也必然有一定宽度，称为谱线的自然宽度。(www.daowen.com)

二、波函数

不确定关系式（14-23）表明，微观粒子在某一方向上的位置和该方向动量的分量不能同时取确定值。因此，对于微观粒子来说，运动轨迹的概念不再有意义。从而经典力学中描述宏观客体运动状态的方法也就不再适用于微观客体。

为了寻求微观客体的状态的描述方法，我们讨论理想的弱电子衍射实验，让电子几乎一个一个入射到狭缝，观察单个电子的作用。每个电子都仅射到观察屏上某一点，在照相底片上产生一个黑点。说明电子和屏相互作用时，保持了其整体性，而且实验表明，个别电子打在屏的什么地方是不能预言的偶然事件。当屏上打上去的电子数不多时，照相底片上出现杂乱无章分布的一个个黑点；而当电子打到屏上的数目多很多时，那些分散的无规则分布的黑点，汇集成了和强电子实验的衍射图样完全一样的衍射条纹。照相底片上的黑环是电子碰击多的地方；白环是电子不碰击的地方，并且具有可重复性。从波动观点，黑环是波场强度极大处，白环是波场强度极小处。由此可见，波场强度（与振幅平方成正比）大的地方电子出现的概率大；波场强度为零的地方，电子出现的概率为零。实验指出，电子的波动性是许多电子在实验中的统计结果，或者是单个电子在许多次相同的实验中的统计结果。

概括对物质世界的认识，对于光的认识首先统一到波动性（电磁波），然后认识到其粒子性（光子）；对实物粒子，则首先认识到它的粒子性（电子、原子、分子……），然后认识到它的波动性（物质波）。粒子性是指物质相互作用的定域性和整体性，可以用能量、动量等物理量来描述，但不是经典粒子，而是微观客体。它在某处出现是偶然事件，用概率描述，与“粒子运动有确切轨道”没有什么必然联系。波动性是指波场传播的弥散性，可以用波长、频率等物理量描述，具有相干叠加性。它不是经典意义上的波，并不是一定要与某物理量在空间分布联系在一起，它只是一种比较抽象的概率波，其波场强度与微观客体出现的概率成正比。在上述意义下说微观客体具有波粒二象性，它是物质的基本属性。对微观客体的状态描述，必须能反映这一基本属性，能描述微观粒子运动的统计规律性。

微观粒子的状态用波函数描述，波函数是一个随时间和空间而变化的函数，用ψ（r, t）表示，r是矢径。波函数所描述的是与微观粒子相联系的物质波。根据波动理论，波场强度I与振幅的平方成正比，即有

由电子衍射实验知道，微观粒子在空间某处出现的概率P与波场强度成正比，因而与该处玻函数模的平方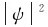成正比，即

式（14-26）给出了波函数的统计解释，即德布罗意波的统计解释。这一解释是玻恩（M.Born，1882—1970）于1926年提出的。更确切地说，如果在空间某一小区域x→x+dx, y→y+dy, z→z+dz内，发现粒子的概率为dP，则

其中，dV=dxdydz为体积元，k为归一化常数。根据德布罗意波的统计解释，要求任意时刻粒子在整个空间出现的总概率为1，即要求波函数满足归一化条件：

将k值代回式（14-27），得

若波函数是已经归一化了的，上式可简化为

式中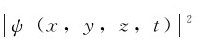，为t时刻r附近单位体积内粒子出现的概率，即概率密度。

从式（14-29）看出，相差一个常数的两个波函数，给出相同的概率分布，描述粒子的同一物理状态。而经典波（电磁波、声波等）波幅增加1倍时，波的能量将为原来的4倍，代表两个完全不同的波动状态。

波函数的数学形式由微观粒子所处的物理条件决定，一般为空间和时间的复变函数。由于概率波的概率解释，波函数ψ（r, t）还要满足一定数学上的条件：在空间某处某时刻粒子出现的概率，应当是唯一的，故波函数应该是空间和时间变量的单值函数；规一化条件要求波函数是平方可积的，即有限的；再者，粒子在不同区域的概率分布应当是连续的，不能逐点跃变。因此，波函数应是空间变量的连续函数。波函数应是r、t的单值、有限、连续函数，称为波函数的标准条件，或自然边界条件。