§14-4　实物粒子的波粒二象性

一、德布罗意物质波假设

1924年，德布罗意在自己的博士论文中首次提出物质波的假说：一切实物粒子都具有波粒二象性，与实物粒子相联系的波称为物质波，即德布罗意波。一个具有能量为E和动量p的实物粒子，与物质波的波长和频率的关系为

式（14-17）和式（14-18）称为德布罗意关系，或称为爱因斯坦—德布罗意关系。其中ω、k为物质波的圆频率和波矢。

设自由电子的能量为E，粒子的速度远小于光速，则E=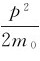，由式（14-18）可知其德布罗意波长为

如果初速度为零的电子，经U伏的电势差加速，则E=eU电子伏，e为电子电荷的大小，将h、e和电子质量m₀数值代入式（14-19）可得

由上式可知，当电子被150V的电势差加速时，德布罗意波长为0.1nm，此波长与原子的线度、固体中相邻原子的间距，以及X光的波长都是同数量级的。这一方面说明为什么电子的波动性长期没有被发现的原因，另一方面也给出了观察电子波动现象要具备的条件。

二、电子衍射实验(www.daowen.com)

德布罗意假设被许多实验所证实。1927年戴维森（C.J.Davisson）和革末（L.H.Germer）用类似X射线在晶体表面衍射的方法，成功地观测了电子衍射实验。图14-9是汤姆孙（G.P.Thomson）电子衍射实验示意图。电子束通过厚度10-15cm金属箔片后，在观察屏上形成图14-9所示的环纹，它与X射线衍射图样十分相似。

把电子束看成与X射线一样，由相邻两个晶面反射，其光程差如图14-10所示

δ=2dsinφ

式中，d为相邻的晶面间距离，φ为掠射角，只有满足条件

电子束才能加强，否则反射将相消。式（14-21）称为布喇格条件。将式（14-20）代入上式中，可得电子束反射强度。取极大值时与加速电压的关系

由上式可以算出各极大值点所对应的电压U值，结果与实验完全符合。

图14-9表明电子束通过晶体后与X射线有完全类似的现象，即产生衍射现象。衍射是波动的基本特征之一，从而证明了电子有波动性。通过电子衍射图样的测量，测得的结果与德布罗意在理论上所预言的完全一致，物质波的假说和德布罗意关系得到了实验证实。