§14-3　康普顿效应　光的波粒二象性

一、康普顿效应

早在1912年，萨德勒（C.B.Sadler）等人就发现X射线被轻元素的电子散射后，波长有变化的现象。1923年，康普顿（A.H.Compton）经过对X射线被物体散射的深入分析，建议把X射线散射波长变长的现象看成是光子和电子碰撞而产生的，这种现象称为康普顿散射或称为康普顿效应。此后，康普顿与我国物理学家吴有训一起，用实验方法完全证实了上述看法的正确性。

图14-7（a）是康普顿实验装置，图中由X射线管发出的单色X射线，通过光阑D1、D2成为一束狭窄的光束，投射到散射物质（石墨等）上，散射波长用布拉格晶体反射测量，散射光强用探测器（如电离室）测量。图14-7（b）是实验结果。由图可知波长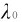的入射线，经过散射后，各方向的散射线中除原波长外，都出现了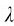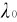＞的谱线；波长差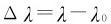随散射角θ的增加而增加。对于不同元素的散射物质，在同一散射角下，波长差Δ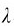相同，波长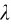的谱线强度随散射物的原子序数的增加而减小。

按照经典电磁理论，当频率一定的单色电磁波作用在带电粒子上时，带电粒子将以入射电磁波的频率做简谐振动，而向各个方向发射出散射电磁辐射，散射电磁辐射和入射电磁辐射有相同的频率和波长。经典理论无法解释散射光的波长变化的现象。

康普顿利用光子理论圆满地解释了上述实验结果。光子理论认为X射线散射可以视为是单个光子和单个电子间的完全弹性碰撞，碰撞前电子是自由电子，相对光子（能量10⁴～10⁵eV）而言电子（能量百分之几电子伏特）可以看成是静止的。在碰撞过程中，能量和动量守恒：

hν₀+m₀c²=E_e+hν

p₀=p_e+p

式中，ν₀和ν分别表示光子碰撞前后的频率；p₀和p分别是光子碰撞前后的动量；m₀c²是电子的静止能量；p_e和E_e分别是电子碰撞后的反冲动量和能量，如图14-8所示。将式（14-14）平方除以c²，再减去式（14-15）的平方得

考虑相对论中电子能量与动量的关系

以及光子的能量和动量间的关系

则有

[（p₀-p）+m₀c]²-（p₀-p）²=m²₀c²

上式化简得

（p₀-p）m₀c-p₀p+p₀·p=0

利用关系式p=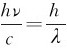，上式变为

其中，θ为p₀和p的夹角，即光子的散射角。经整理上式变为

设

称为康普顿波长，是一个常量，电子的康普顿波长为2.43×10^-12M.最后，得到波长随散射角θ而改变的关系式：(www.daowen.com)

利用光子和电子碰撞的机制所得到的公式（14-16）与实验结果符合得很好。不仅直接证实了光子的客观存在，而且还表明，在微观粒子碰撞过程中，动量和能量守恒定律仍然成立。康普顿的理论和实验确认了普朗克、爱因斯坦揭示出的光的微粒性，即光的量子性。

在讨论中认为电子是自由电子，实际上原子中的电子被核束缚并不一定很弱，尤其是原子内层电子被束缚得相当紧。光子与这种电子碰撞时，实质上是和质量很大的整个原子交换能量和动量。散射过程中光子只改变方向，能量几乎不变。因此，散射光中总存在原波长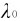的这条谱线。随着碰撞原子的原子序数的增加，散射光子的能量接近不变，所以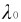的强度则随之增加，而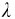的强度则随之减小。

二、光的波粒二象性

在光学发展史上，对光的本性的认识存在粒子和波动两种观点。麦克斯韦电磁理论建立后，认为光是以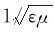的速度在介质中传播的电磁波。当时，所知道的一切光学现象，几乎都能纳入电磁理论，即光的波动理论。关于光的本质的认识，波动理论战胜了牛顿的微粒论，似乎统一到了波动观点上。然而，19世纪末，人们研究光与物质相互作用时，发现了黑体辐射、光电效应等一系列新的实验结果又揭示出了光的量子本性。最后，把对光的本性的认识统一到光的波粒二象性，建立了光的量子理论。

光的量子理论的基本观点是：光是由光子组成，频率为ν的光的每一光子，具有能量Ehν和动量p=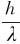n，光子的运动遵从麦克斯韦电磁场方程，呈现波动性。但光波不再是经典意义上的波，而是一种具有统计规律性的电磁波，光子也不是经典意义上的粒子，它在某处出现是偶然事件，用概率描述。在这种意义上，我们说光具有波粒二象性。光的波粒二象性表明，光的波动性表现为具有干涉、衍射现象，传播过程中具有弥散性，能用波动的基本要素（波长、频率）来描述；粒子性表示为光与物质相互作用时，具有定域性或整体性，可用粒子的基本要素（能量、动量）来描述。波动性和粒子性的统一性表现为波场强度和光子出现的概率成正比，光子的能量和动量分别由hν和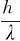n表示。

光的波粒二象性是人类对光的本质认识的深化，光的波粒二象性是光具有的统一性。光的这种性质既不是经典波动性和经典粒子性的简单凑合，也不是二者的符合，它是通过系列实验事实，人们才认识到的光的本质属性。

例14-3　设有波长为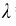=0.1nm的X射线的光子与自由电子做完全弹性碰撞，在散射角为60°和90°方向观测时，求：

（1）散射波长的改变量Δ；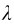

（2）反冲电子的动能；

（3）碰撞过程中，光子的能量损失；

（4）讨论散射角变化对上述三个量的影响。

解　（1）由公式（14-16）得

当θ分别为60°和90°时，有

（2）由式（14-14）可知

式中，E_e是反冲电子能量；m₀c²是碰撞前电子的静止能量。所以，反冲电子的动能为

散射角为60°和90°时，反冲电子的动能分别为

（3）光子损失的能量等于反冲电子所获得的动能，即反射角为60°时，光子损失能量为1.21×10^-27J；散射角为90°时，光子损失能量为4.71×10^-27J。

（4）从以上运算可知，当散射角增大时，波长差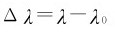增加；反冲电子的动能随散射角的增大而增加。实际上，这些结论，从对式（14-16）和式（14-14）的分析可立即得到。