§14-2　光电效应　光的量子性

当光束照射在金属表面上时，金属中的电子吸收光能而脱出金属表面的现象，叫光电效应。

一、光电效应的实验规律

图14-4给出研究光电效应的实验装置图，阳极A和阴极K被封装在玻璃泡内，玻璃泡被抽成真空，且开有石英窗，其整体构成一个真空光电管，两极加有连续可调的电压U，并且能改变符号。A为电流计。

一定频率的光通过石英窗照射到阴极K上，K中获得足够能量的自由电子，脱出金属表面，在加速电场的作用下，向阳极A定向运动形成电流。由于光照脱出的电子叫做光电子，形成的电流叫光电流。光照越久光电流维持的时间就越长；停止光照，回路中没有电流。观测实验结果，得到如下主要规律。

1.单位时间内，由阴极发出的光电子数和光强成正比

在一定的光强照射下，光电流I随着光电管两极间的加速电压U的增大，逐渐趋于一个饱和值；而光强增大时，饱和电流随之增大，饱和光电流与光强成正比，图14-5所示是光电流伏安特性曲线。

2.光电子的初动能随入射光频率的增大而增大

如果将加速电压U降低为零，光电流不为零，甚至电源反向，使两极间形成减速电场时，光电流仍不为零，当反向电压增大到一定值U₀时，光电流才减小为零。U₀称为遏止电压。实验表明，遏止电压与光强无关，如图14-5所示中曲线。对应的光强不同，光电流在相同的反向电压U₀下被完全遏止。

实验表明，从阴极发射出的光电子有一定的初速度。一定频率的光所释放光电子的初动能上限由下式决定：

式中，m为电子质量；e为电子电荷绝对值。式（14-9）说明，光电子的初动能等于它们克服减速电场的阻碍所做的功。

改变入射光的频率ν时，遏止电压U₀随之改变，U₀与ν呈线性关系，如图14-6所示。考虑式（14-9）中U₀与电子初动能的关系，得到光电效应的第二条规律：光电子的初动能随入射光的频率的增大而增大，而与入射光的强度无关。

3.截止频率

图14-6所示表明，入射光的频率ν降低时，U₀随之减小，ν低于某一频率ν₀时，U₀亦为零，此时无论光强多大，光电效应都不会发生。频率ν₀称为截止频率，或称频率的红限。截止频率ν₀由光电阴极材料决定，与光强无关。

4.弛豫时间

当入射光照射到光电管阴极上时，从光照开始到光电子发出，所经历的时间称为光电效应的弛豫时间。实验发现，只要入射光的频率大于频率红限ν₀，无论光强如何微弱，光电效应几乎是瞬时发生的。经过准确测量，弛豫时间不超过10^-9s。

二、爱因斯坦光子假说

根据经典电磁理论，当光照射到金属上时，金属中的电子做受迫振动，直到电子的振幅足够大时，脱出金属表面而溢出。光电子的能量等于它吸收的光能减去金属的脱出功，电子每单位时间吸收的能量与光强I成正比。设从开始光照到电子从金属表面溢出经历的时间为Δt，则电子积累的能量与IΔt成正比。因此，按照光的波动理论，光电子的能量在弛豫时间一定的情况下，应与光强成正比，而与光的频率无关。无论光强多么微弱，只要时间足够长，电子总是可以积累到溢出金属表面的能量。这样，经典物理学理论既不能解释光电子初动能与入射光频率的线性关系，也不能说明截止频率存在，更无法解释光电效应瞬时性发生的原因。鉴于经典物理学与光电效应实验规律的尖锐矛盾，爱因斯坦汲取普朗克能量子的观点，于1905年提出光量子，即光子假说：辐射场由光量子组成，每个光量子的能量与辐射场的频率的关系为

E=hν

由狭义相对论知道，以速度v运动的粒子的能量为

式中，m₀为粒子的静止质量。对于以光速传播的辐射，光量子v=c，所以光子的静止质量为零。光的能量与动量之间的关系为

E=cp(www.daowen.com)

以光速运动的光子不但有能量

而且有动量

式中，n为光子运动方向的单位矢量；k=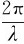n为波矢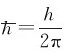；=1.0545×10^-34J·s。采用光子概念之后，光电效应的实验规律得到了圆满解释。

当光照射到金属上时，金属中的自由电子吸收一个光子。只要入射光频率足够高，即每个光子的能量E=hν足够大时，电子就可以克服脱出功A而逃逸出金属表面成为光电子。按照上述理念，爱因斯坦提出了后人以他的名字命名的爱因斯坦光电效应方程：

上式表明，金属中的每个电子吸收一个光子，所获得的能量E=hν除了用以逃逸金属表面克服脱出功之外，便是光电子逸出金属表面后的初动能。

光子理论对光电效应实验规律作出了如下的解释：入射光强与光子流密度成正比，光强大表明入射到金属上的光子流密度大。单位时间内，金属中就可能有更多的电子吸收光子能量而逃逸出金属表面，因而饱和光电流大。每个光电子吸收一个电子获得能量E=hν，所以光电子的初动能随频率的增大而增大，而与光强无关。由式（14-13）可以看出，对一定材料的光电阴极，有确定的脱出功A。当入射光频率一定时，相应光电子的初动能也是一定的，对应一个确定的遏止电压。因此，不难理解，遏止电压与频率呈线性关系的实验规律。当入射光的频率为某一频率ν₀时，使得h_ν0=A，电子吸收的能量刚好够克服脱出功，电子脱出金属表面后，初动能为零。若入射光频率ν＜ν₀，电子吸收光子的能量h_ν0＜A，电子便不能逸出金属表面，光电效应不能发生，从而解释了截止频率ν₀=A/h。此外受到光照的金属中的自由电子，要么吸收一个光子hν（ν＞ν₀）逃逸出金属表面，要么不吸收光子，仍留在金属内做热运动。电子同时吸收两个光子的概率几乎为零。电子获得光能不需要时间积累，所以光电效应的发生是瞬时性的。

1916年密立根（R.A.Millikan，1868—1953）研究了Na、Mg、Al、Cu等金属，得到遏止电压与频率之间的严格线性关系，并由直线斜率

测得普朗克常量h的精确数值，与黑体辐射等实验测得的数值完全符合，从而证实了爱因斯坦对光电效应解释的正确性。

上述光电效应中电子逸出金属，所以称为外光电效应。利用光电效应的原理制成的各种光电器件，如光电管、光电倍增管及摄像管等，广泛地用于光信号的记录和测量、光电信号的转换及各种自动控制设备。另一类光电效应，如光照射到某些半导体材料被吸收，其内部激发出导电的载流子（电子—空穴对），改变了材料的导电性能，使其导电率显著增加，这种现象称为光电导。光生载流子的运动，也可造成电荷聚集，使材料两面形成一定的电势差，即所谓光生伏特，这些现象称为内光电效应。利用内光电效应研制的光敏电阻、光电池及光电二极管等光电器件，早已广泛应用。

例14-1　试计算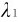=500nm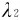，=0.1nm和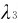=0.0001nm相对应的光子能量。

解　根据式（14-11）及波长与频率的关系

光子的能量分别为

同理计算得

例14-2　某一光电管在两种不同的单色光照射下，测得遏止电压分别为-0.30V和-2.30V。已知单色光之一是纳光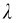（=589.3nm），问另一单色光的波长为多少?

解　由爱因斯坦光电效应方程式（14-13）得，波长为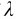的光的光子能量为

hν=eU₀+A

因此，对于题设中的两种单色光分别有

hν₁=eU₀₁+A

hν₂=eU₀₂+A

上两式相减，并考虑关系ν=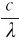，得

整理得