一、绝对黑体

19世纪末，由于冶金测高温技术及天文学方面的需要，推动了对热辐射的研究。当时已经认识到热辐射是电磁波。所有物体在任何温度下，都以电磁辐射的形式辐射能量。物体发射能量的多少，以及辐射能量按波长的分布，都与发射体的温度有关。因此，这种辐射称为热辐射。对外来的辐射，物体有吸收和反射的作用（若物体是透明的，则还有透射的作用）。如果一个物体能够全部吸收而不反射投射于其上的辐射，该物体就称为绝对黑体，简称黑体。

在自然界中，不存在绝对黑体。实际上，投射到物体上的辐射总是有一部分被反射。绝对黑体只是一种理想化模型。如图14-1所示，一个空心容器上开一个小孔，小孔的孔面可以近似地视为绝对黑体。当射线射入黑体后，被空腔内壁多次反射后，才可能从小孔射出，射出能量与射入能量的比为

（1-α）ⁿ

其中，α为内壁每一次反射吸收能量和入射总能量的比值，称为物体的吸收比。当内壁反射的次数n足够大时，（1-α）ⁿ近似为零。则小孔孔面吸收比近似为1，进入小孔的射线全部被吸收。小孔孔面是很好的绝对黑体的模拟，空心容器处于某确定温度时，小孔可以发射出各种频率的辐射，从小孔发射出来的辐射能够当做黑体表面的辐射，其表面面积就等于小孔的孔面积。事实上，在黑体辐射实验中，正是利用空心容器的小孔发射作为绝对黑体的辐射。

为了描述各种物体的热辐射，引入单色辐射出射度的概念。在单位时间内，从温度为T的物体单位面积上，所发射的频率在ν到ν+dν范围内的辐射能量为dEν，定义dEν与频率间隔dν的比值

为单色辐射出射强度，简称单色辐出度。它表示在一定的温度下，辐射能量按频率分布的情况。单位时间内，从物体表面单位面积上所发射的各种频率的总辐射能量，称辐射出射度，简称辐出度，它与单色辐射出射度的关系为

利用空心容器可以测定绝对黑体的单色辐出度。实验中，在热平衡状态下，测得绝对黑体的单色辐出度按频率分布的曲线，如图14-2所示。

二、斯忒藩—波耳兹曼定律维恩定律

1.斯忒藩（J.Stefan）—波耳兹曼（L.Boltzmann）定律

实验表明，绝对黑体的单色辐出度I_B（ν，T）是热力学温度的函数，而与黑体的材料无关，当黑体的温度为T时，它的辐出度E_B（T）等于该温度下I（ν，T）-ν曲线下的面积。温度升高时，黑体的辐出度随之增大。由实验曲线可得黑体辐射的辐出度

E_B（T）=∫^∞₀I_B（ν，T）dν

与温度的四次方成正比，即

E_B（T）=σT⁴

这一规律称为斯忒藩—波耳兹曼定律，σ是一个普适常数，称为斯忒藩—波耳兹曼常量，实验测得σ=5.670×10^-8W/（m²·K⁴）。由式（14-3）可知，黑体的辐出度随温度的升高而急剧增加。

2.维恩（W.Wien）位移定律

图14-2中的曲线表明，在任何温度下，IB（ν，T）-ν曲线都有一极大值，即单色辐出度频率曲线的峰值。设极大值对应的频率为νm，随黑体温度T的升高，νm向高频方向移动，即峰值所对应的波长向短波方向移动。维恩发现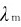，与T成反比：

其中，b是个普适常数。实验测得

b=2.898×10^-3m·K

称为维恩常数。式（14-4）给出的规律为维恩位移定律。(www.daowen.com)

维恩位移定律给出了热辐射的颜色和温度的定量关系，由式（14-4）可知，当温度不太高时，辐射中绝大部分是红外线，其中包含一小部分红光；随着温度的升高，峰值波长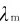向短波方向移动，辐射则由红变黄，温度高达5000～6000K范围内时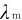，位于可见光波段的中部。此时热辐射中全部可见光都较强，它引起人眼的感觉是白光，如太阳光谱的连续部分的峰值位于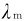=460nm的地方，约相当于T=6000K的辐射光谱，所以太阳光是白光。

三、维恩公式　瑞利—金斯公式

为了从理论上导出符合实验曲线I_B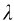（，T）的函数形式，19世纪末，许多物理学家从经典物理学理论出发，做了相当大的努力，但都遭到了失败，没有得到与实验结果相符合的理论公式，其中最典型的是如下两个公式：

1.维恩公式

1896年，维恩用辐射按波长分布的思想，得出一个理论公式：

称为维恩公式，其中c₁、c₂为常数。式（14-5）与实验曲线比较，短波区域符合得很好，而长波范围则有系统性偏差，如图14-3所示。

2.瑞利—金斯公式

瑞利（J.W.S.Rayleigh，1842—1919）和金斯（J.H.Jeans，1877—1946）把经典热学的知识用到电磁辐射，得到另一个公式

其中，c₃为常数。式（14-6）与实验曲线比较，长波区域符合得较好，而在短波部分偏离得非常大，如图14-3所示。

由此看出，当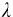→0时，I_B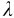（，T）→∞，即波长极短的辐射（光谱的紫外部分）单色辐出度趋于无穷大。金斯经过深入研究，断言：只要坚持经典统计理论，式（14-6）及上述的结论就是不可避免的。经典理论与实验的这一尖锐矛盾，动摇了整个经典物理学理论，鉴于其引起的严重后果，历史上称为“紫外灾难”。正是这一物理学的灾难预告了量子论即将诞生的“福音”。

四、普朗克公式　量子假设

正确的黑体辐射公式是普朗克提出的。普朗克认为：既然维恩公式和瑞利—金斯公式分别与实验的高频部分和低频部分相符合，只要把两个公式连接起来，就会得到与整个实验曲线一致的理论公式。普朗克首先用内插法，将维恩公式和瑞利—金斯公式衔接起来，然后再加以理论论证。

普朗克把黑体（空腔容器模型）视为大量的谐振子组成的系统。经过发射和吸收，谐振子和辐射场交换能量。但与经典物理不同，普朗克假设：谐振子吸收和发射的能量，只能是某一最小能量ε₀的整数倍，即

ε=ε₀，2ε₀，3ε₀，……，nε₀

式中，n称为量子数，最小能量ε₀称为能量子，它与简谐振子的频率ν成正比，即

ε₀=hν

式中，比例系数h称为普朗克常量，它的国际公认值为h=6.626×10^-34J·s。普朗克按照他的上述能量子假说，并利用统计理论推导出了与实验结果符合得很好的公式

式中，c是光速，k是波耳兹曼常量。

普朗克的能量量子化假设是对经典能量观念的一次革命。从经典物理学看来，能量是连续的，能量子的假设是不可思议的。就连普朗克本人在提出量子概念后，还长期试图用经典物理学来解释其由来，这导致他对量子理论的发展，没有作出进一步的贡献。但是无论如何，普朗克给物理学引进量子，第一次揭示了微观物体与宏观物体有着根本不同的性质，使人们对微观世界的认识大大地深入了一步，具有深刻的革命意义。