§13-3　相对论动力学

从相对论运动学中已知，在高速运动的情况下，时空的性质变了。由于物质的运动和时空的性质紧密相关，因而，物质的高速运动规律也会有相应地改变。这就是相对论动力学所要讨论的内容。

一、质量和动量

在经典力学中，物体的动量定义为其质量和速度的乘积，即p=mν。动量守恒定律是已经被大量实验事实所证实的基本规律。对于这种普遍性的规律，在相对论中也应成立。但是，若仍然像经典力学那样，把物体的质量当成与其运动状态无关的恒量，在洛伦兹变换下，它就不能对所有惯性系都成立。因此，在相对论中，就必须放弃原有的经典力学观点，认为质量与速度相关。但由于空间的各向同性，质量仅是速率的函数而与速度的方向无关。

可以证明质量随速率变化的关系为

这就是相对论中的质速关系式。于是，在相对论中，物体的动量表达式为

由此可见，当物体的速率远小于光速时，其运动质量都近似等于其静止质量，即可近似地看做常量。而当物体的速率趋近于光速时，其运动质量将趋于无穷大，动量也趋向无穷大。这时就很难被外力再加速了。这就是光速c是物体的极限速率的动力学原因。

二、相对论动力学的基本方程

在经典力学中，牛顿最初提出的动力学基本方程就是用动量p=mν来描述的，即

在相对论中，这种关系不变，但根据式（13-8），相对论动力学的基本方程应改写成如下形式

当v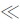c时，式（13-10）则近似简化为

即为牛顿第二定律的形式。这表明，相对论动力学的基本方程是更具有普遍性的动力学关系。

三、质量与能量的关系

在相对论中，牛顿力学的动能定理仍然适用，即物体的动能增量等于合外力对它做的功。

今设静止质量为m0的物体，从静止开始，在外力F的作用下沿x轴运动。当其速率达到v时，动能为Ek。根据动能定理的微分形式有

积分得

化简得

E_k=mc²-m₀c²(www.daowen.com)

式中，m为动质量；m0为静止质量。由E_k=（m-m₀）c²=Δmc²可知，物体的动能与由运动引起的质量增量成正比。

当物体低速运动，即v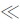c时，对式（13-11）利用二项式定理展开可得

略去高次项近似可得

这就是牛顿力学的动能表达式。这表明，从能量角度也说明牛顿力学是相对论力学在低速情况下的近似。

式（13-11）也可写做

mc²=E_k+m₀c²

其中，m₀c²为物体静止时的能量，称为静能；mc²则为物体动能与静能的总和，称为物体的能量E。即

E=mc²

这就是狭义相对论的质量与能量的关系。它反映了物体的质量和能量是相互关联的，是不可分割的。质量的改变就意味着能量的改变，能量守恒也就意味着质量守恒。

四、能量和动量的关系

设静止质量为m₀的物体，以速度v运动。则其动量和能量分别为

两式平方相除可得

即

整理可得

E²=m²₀c⁴+p²c²

这就是相对论中的能量和动量的关系式。可以用一个直角三角形的勾股弦形象地表示这一关系，如图13-6所示。