§12-7　热力学第二定律的统计意义　熵

一、热力学第二定律的统计意义

热力学第二定律指出，一切与热现象有关的实际过程都是不可逆的，自然过程都有一定的进行方向。这种不可逆性可以从微观上来解释其统计意义。

我们知道，气体可以自动膨胀，但不会自动收缩。这就是一种统计规律。设想有一容器，由活动隔板等分为A、B两室，如图12-14所示。起初A室中充有气体，B室为真空，此时气体分子只能在A室内运动。把隔板去掉后，分子则可在整个容器中随机运动。由于A、B两室相同，所以，每个分子处于A室和B室的概率各占50%。假定总共有a、b、c、d四个分子，它们在A、B室共有16种分配方式，其具体情况见表12-2所列。

表12-2　气体分子占据空间的分配方式

从宏观上描述系统状态时，只能以A或B室中分子数目的多少来区分系统的不同状态，但却无法区别A和B室中到底是哪些分子。我们把A、B室中分子数的不同分布称为一种宏观态，而把能够区分A、B室中是哪些分子的分配方式称为一种微观态。显然系统的每一种宏观态可以包含有许多微观态。例如，4个分子全部位于A室中这种宏观态只包含一个微观态，而3个分子位于A室，1个分子位于B室的宏观态包含有4个微观态。

统计理论认为，孤立系统内各微观状态出现的机会是相同的，即等概率的。在给定宏观条件下，系统存在大量各种不同的微观态，每一宏观态又包含有许多微观态，而各宏观态所包含的微观态数目并不相同。因此，各宏观态的出现就不是等概率的了。由表12-2可知，微观态数总共有Ω=16=2⁴个。如分子全部集中在A室的宏观态只有一个微观态，出现的概率只有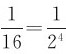；而两室内各有两个分子的均匀分布的宏观态所含微观态数目最多，为6个，出现概率最大有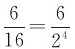。如果系统有N个分子，同样分成A、B两部分，可以推论其总微观态数应为2^N个，N个分子同时退回A室的宏观态，概率仅为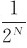；再如，1mol气体的分子数为6.023×10²³个，气体自由膨胀后，所有分子退回A室的概率为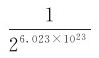，概率如此之小，实际上根本观察不到。而分子处于均匀分布的宏观态，出现的概率最大。所以，自由膨胀过程实际上是由包含微观态数少的宏观态向包含微观态数多的宏观态进行。这一结论对所有自然过程都是成立的。

概括上述分析可知，一切自然过程总是由包含微观态少的宏观态向包含微观态数多的宏观态方向进行，这就是热力学第二定律的统计意义。

二、熵

统计物理学定义：宏观态所对应的微观态数称为该宏观态的热力学概率，用希腊字母Ω表示。从前面的讨论可知，分子全部分布在A区或B区的这种宏观态热力学概率最小；而均匀分布的这种宏观态的微观态数目最多，即热力学概率最大。可以证明，当微观粒子数增多时，相对均匀的微观态数目所占比例会增大，均匀分布出现的概率会迅速增加。因此，热力学系统在处于平衡态时，对应的均匀分布的概率占了绝对优势，接近百分之百，而相对不均匀的分布几乎不存在，完全可以忽略。(www.daowen.com)

从前面讨论可知，自然过程总是使分子运动向更加无序的方向进行，即自然过程是往热力学概率Ω增加的方向进行，当达到Ω_max时，该过程就停止了。两种说法相比较，可知热力学概率Ω是分子运动无序性的一种量度。因此，玻耳兹曼引入一个态函数熵，用S表示，其与热力学概率Ω的关系为

S=klnΩ

称为玻耳兹曼熵，k为玻耳兹曼常数，熵的单位是J/K。

熵是系统的态函数，对于热力学系统的每一宏观态，都有一热力学概率Ω值对应，也就有一个熵值S对应。和Ω一样，熵的微观意义是系统内分子热运动无序性的一种量度。

用S代替Ω后，热力学第二定律可以用熵来描述：在孤立系统中所进行的自然过程总是沿着熵增加方向进行，这就是熵增加原理。数学表示为

ΔS＞0

因为自然界中实际发生的过程都是不可逆的，由熵增加原理可知，孤立系统内发生的一切实际过程，都会使系统的熵增加。即在孤立系统中，一切实际过程只能朝熵增加的方向进行，直到熵达到最大值为止。虽然熵增加原理限于孤立系统成立，因为任何一个热过程，总可以把过程所涉及的物体都视为系统的一部分，则对于该过程系统就变成了孤立系统，过程中系统的熵就一定满足熵增加原理。因而，实际上熵增加原理是一个十分普遍的规律。应强调指出，熵增加原理是指组成孤立系统的所有组成部分熵之和的增加。而对于孤立系统内的个别部分来说，热过程中它的熵增加、减少或者不变都是可能的。

由于熵增加原理与热力学第二定律都是阐述热过程自发进行的方向和条件，所以熵增加原理是热力学第二定律的数学表达式，式（12-23）提供了判别一切过程进行方向的准则。