§12-4　绝热过程

系统不与外界交换热量的状态变化过程称为绝热过程。实际上，完全的绝热过程是不存在的。但是在有些过程中所传递的热量很少，可以忽略不计；有些过程进行得很迅速，致使系统来不及与外界交换热量。例如，用气筒打气、气体爆炸等。这样的过程都可以近似看做绝热过程。

在绝热过程中，dQ=0，故由热力学第一定律可得

0=dE+dW=dE+pdV

或写成

dW=pdV=-dE

由此可见，在绝热过程中，系统是凭借消耗其内能来对外界做功的。

根据式（12-11）可知，dE=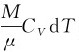，代入上式可得

对理想气体状态方程pV=RT两边取微分得

上式两边乘C_V，再与式（12-15）比较，得

C_V（pdV+Vdp）=-RpdV

考虑到R=C_p-C_V，γ=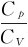，整理可得

积分可得

lnp+lnV^γ=ln（pV^γ）=常量

即有

pV^γ=常量(www.daowen.com)

将理想气体状态方程pV=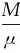RT代入上式，分别消去p或V，可得

V^γ-1T=常量

p^γ-1T^-γ=常量

式（12-16a）、式（12-16b）、式（12-16c）统称为理想气体的绝热过程方程，简称绝热方程。三个方程中的常量均不相同，使用时可根据处理问题的方便，任取其中一个应用。

由式（12-15）积分可求得理想气体在有限绝热过程中做的功为

将γ=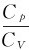代入上式，可得

如图12-7所示的等温线和绝热线，过A点同一气体的等温线分别由绝热过程方程pVγ=常量和等温过程方程pV=常量作出。可以看出，通过同一点的绝热线（实线）比等温线（虚线）陡些。下面对两条线交点A处斜率通过计算加以讨论。对绝热过程和等温过程方程取微分可得

γpV^γ-1dV+V^γdp=0 pdV+Vdp=0

由此可得，在p-V图中绝热线和等温线的斜率为

由于γ＞1，故绝热线斜率的绝对值大于等温线斜率的绝对值，即绝热线比等温线更陡些。这是因为在等温膨胀时，压强的降低Δp_T仅由气体密度减小而引起，而绝热膨胀时，除气体密度减小外，气体的温度也要降低。所以Δp_S＞Δp_T。

例12-1　氮气液化，把氮气放在一个有活塞的绝热壁包围的汽缸中。开始时，氮气的压强有50倍标准大气压，温度为300K。经急剧膨胀后，其压强降至1倍标准大气压，从而使氮气液化。试问此时氮气的温度是多少?（1标准大气压=1.013×10⁵Pa）

解　把氮气视为理想气体，其液化过程可当做绝热过程。由题意知p₁=50×1.013×10⁵Pa,T₁=300K,p₂=1×1.013×10⁵Pa，由表14-1可查得氮气的γ=1.40。所以按绝热方程式（12-16c）可得

将已知数据代入上式，有

T₂=300×0.02^0.286=98.0K

这个值只是大略的估计值。因为在低温时氮气不能再视为理想气体，而且把氮气的膨胀过程视为绝热过程也只是近似的。