§11-2　起偏和检偏　马吕斯定律

一、偏振片起偏和检偏

除激光器等特殊光源外，普通光源发出来的光都是自然光。把自然光变为偏振光称为起偏。在实际应用中最简单的一种起偏方法是利用偏振片获得偏振光。从自然光中获得线偏振光的装置称为起偏器。偏振片是最简单的起偏器。

当今广泛应用的人造偏振片是在透明的基片上涂敷一层某种物质（如硫酸金鸡钠碱、碘化硫酸奎宁等）晶粒制成的。这种按一定方向排列的微晶物质，能吸收某一方向上的光振动，而只允许与之方向垂直的光振动通过。这一允许通过的特定振动方向称为偏振片的偏振方向，也称透光轴，如图11-5所示。

图11-6表示一束自然光通过偏振片A后成为光振动平行于偏振方向的偏振光。偏振片A的作用是把自然光变为偏振光，偏振片A即为起偏器。

偏振片既可以用做起偏器，使自然光成为偏振光，又可以用来检查某一光是不是偏振光，称为检偏，即又可作为检偏振器。图11-6（a）中自然光通过起偏器A变成线偏振光，射到偏振片B上，B与A偏振化方向相同，则通过A的偏振光仍然透过B，可以清楚地看到放在A、B前的物体。若把B绕光的传播方向转过α角，则既通过A又通过B的光强减弱，如图11-6（b）所示，图像变暗。若将B的转角α=90°，则通过A的偏振光不能通过B，通过A、B的光强为零，当然也就看不到物体了。如果以入射到B上的线偏振光的传播方向为轴，不断旋转偏振片B，就可以观察到光线明、暗交替地变化。如果入射到B偏振片的不是线偏振光而是自然光，以同样的方法旋转B时，透过的光强将无变化，此处偏振片B起到了检查入射光是否偏振光的作用，并同时可以确定线偏振光的振动面，B称为检偏器。

二、马吕斯定律

马吕斯（E.J.Malus）于1809年研究线偏振光通过检偏器后的透射光光强时发现了光强的变化规律。如图11-7所示，设E₀为振动方向沿OM的入射偏振光的光矢量，E₀与偏振片B透光轴ON的夹角为α。将光矢量E₀分解为平行和垂直于透光轴ON的两个分量，则有

E₀=E₁e_∥+E₂e_⊥

其中，e_∥、e_⊥分别为平行和垂直于ON的单位矢量，E₁、E₂为相应的分量。由图11-7（b）看出：

E₁=E₀cosα

E₂=E₀sinα

显然只有平行于偏振方向ON的分量E₁能透过偏振片B。因此偏振光的入射光光强I₀和透射光强I之间存在关系

即

I=I₀cos2α

式（11-3）称为马吕斯定律。它表明：入射线偏振光的光强为I₀，透射过透光轴方向与偏振光的振动方向成α角的检偏器后，透射光的光强I等于α角的余弦的平方和I₀的乘积。

由式（11-3）可知，当转动偏振片B，使B的偏振化方向与入射线偏振光振动方向平行时，即α=0°或180°，I=I₀，透射光最大；当B的偏振化方向与入射线偏振光垂直时，即α=90°或270°，I=0，没有光从检偏器透过，即产生消光现象。若α介于上述两组值之间，则光强介于最大和零之间。

例11-1　如图11-8所示，强度为I₀的自然光，入射到两块相互重叠的偏振片A、B上，如果透射光的强度是最大透射光强度的1/3，问这两块偏振片的偏振化方向的夹角是多少?(www.daowen.com)

解　因入射自然光强度为I₀，则经过偏振片A后的光强为

若两块偏振片的偏振化方向一致，则透射光的最大光强为I₀/2，如图11-8所示。

设透射光强为I₂，由马吕斯定律：

I₂=I₁cos2α

由上述分析结果得

解得

cosα=±0.5774

则

α=54°44′或125°16′

这意味着将偏振片B绕光的传播方向顺时针转过54°44′或逆时针转过125°16′，可以使透射光强减为最大透射光的1/3；若B不动而转动A，可以得到同样效果。

例11-2　用两个偏振片A、B，能否使线偏振光的振动面旋转90°，实验步骤如何?求此时从偏振片B射出的光强最大值。

解　先将偏振片A的偏振化方向N₁与入射线偏振光的振动面呈α（0＜α＜90°）角，再使偏振片B的偏振化方向N₂与线偏振光的振动面垂直，如图11-2所示。于是从B偏振片射出光的振动面与原入射线偏振光的振动面相互垂直，从而使偏振光的振动面旋转了90°。

设入射线偏振光的光强为I₀，通过A、B后的光强分别为I₁、I₂，由马吕斯定律得

I₁=I₀cos2α

所以

显然当α=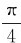时有光强最大值：