§10-2　单缝夫琅禾费衍射

图10-4所示是夫琅禾费单缝实验装置。衍射屏上有一宽度为a，以轴为对称中心的长狭缝K，单色光源S安置在透镜L₁的前焦点上，光源发出的球面光波经L₁后，变成单色平面波垂直入射到衍射屏上，经过狭缝K后产生衍射，再经过透镜L₂聚焦在焦平面处观察屏E上，呈现出一系列平行狭缝的衍射条纹。

这里我们仅用比较粗糙的菲涅耳半波带法来解释夫琅禾费单缝衍射图样。半波带法虽然不够精细，但可方便地得到衍射图样的基本定性特征。

如图10-5（a）所示，单色平行光垂直入射到单缝K的缝平面AB上，作为波阵面AB上的每一点，都发射沿各方向传播的光波，称为衍射光波。沿某一方向的衍射光与狭缝平面法线OP₀的夹角θ称为衍射角。通过A点作平面AC，使其与BC垂直，则单缝边缘A、B两点沿θ方向的衍射光，传到P点的光程差为BC=asinθ。由于透镜不产生附加光程差，所以波阵面AB上各点沿θ方向发射次级光波，传播到AC面的光程差就等于它们传播到屏E上P点的光程差。作一系列平行于AC的平面，使相邻两平面之间的距离为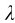/2，则这些平面便将波阵面AB分成了AA₁、A₁A₂、……A_mB等m个窄条带，如图10-5（b）所示，每一窄条带的宽度为

这些窄条带称为半波带。相邻两半波带上的点都是一一对应的，如A₁A₂带上的G₁点对应AA带上的G点。对应点上发出的沿θ方向的衍射光，到达P点时光程差都为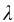/2，即两者在P点引起的相位差为π。由于所有半波带的面积都相等，所以各个半波带在P点引起的光振动的振幅相等。因此任何两个相邻的半波带所发射的光波，在P点叠加将完全相互抵消。

如果整个缝平面对于给定的衍射角θ可以分成偶数（2k）个半波带，而每对相邻的半波带在P点引起的光振动两两相消的结果，从而在屏E上将出现暗条纹。产生暗条纹的条件为

如果整个缝平面对于某给定的衍射角θ可以分成奇数（2k+1）个半波带，半波带在P点引起的光振动两两相消结果还剩一个半波带产生的光振动未被抵消，屏E上将呈现明条纹。产生条纹的条件为

当衍射角θ=0时，则

asinθ=0

表明平行光束无光程差，故会聚于P₀点干涉加强，该位置相应中央亮纹中心。

综上所述，当平行单色光垂直入射时，单缝衍射明、暗条纹的条件为

式中，k为条纹级数，正、负号表示衍射条纹对称分布于中央明纹两侧。

应该指出对于任意的衍射角θ来说，AB不能恰好分成整数个半波带，即BC不一定等于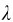/2的整数倍，对应于这些衍射角的衍射光束经透镜会聚后，在屏E上的光强介于最明和最暗之间。因此在单缝衍射条纹中，强度分布不是均匀的。图10-6给出了单缝衍射图样的强度分布曲线。

由式（10-2）得出：各级暗纹和明纹的中心位置对于一定宽度a的单缝，单色光衍射由sinθ决定。图10-6中以sinθ为横坐标，分布曲线由一系列极大和极小组成，它们分别对应各级明、暗衍射条纹。当极大出现在sinθ=0的地方，对应于各衍射光线之间无光程差的情况，此即为几何光学成像点的位置。从波动光学的观点，等光程性保证了到达像点各光线有相同的相位，从而产生最大的强度，所以中央条纹最亮。次级明纹被视为奇数个半波带之一的贡献。随着衍射角θ的增大，被分成的半波带越多，每一波带面积也就越小。因此各级明纹的强度随着级数的增高迅速下降。各级暗条纹出现在

的地方。当衍射角θ甚小时，上式可近似写为

第一级暗纹中心对透镜中心所张的角度为中央明纹的角宽度，当θ很小时由上式知2Δθ=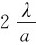，有时也用半角宽度表达中央明纹的宽度：

以f表示透镜的焦距，由于透镜与单缝靠得很近，则在屏E观察到的中央明纹的线宽度为(www.daowen.com)

虽然其他明纹的角宽度均相等且等于中央明纹的半角宽度，即式（10-3）也表示各次级明纹的角宽度，其线宽度为Δx=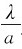f。中央明纹不仅最亮（强度最大），而且衍射斑纹也最宽，它的半角宽度Δθ的大小作为衍射效应强弱的标志。式（10-3）表明：当波长一定时，Δθ与缝宽a成反比。当缝宽越小时，对波阵面上光束限制越大，衍射场越弥散，衍射斑纹拉开的越宽；而当缝宽很大，Δθ→0，衍射场基本上沿原直线方向传播，在透镜焦平面上衍射斑纹收缩为几何光学像点。

在单缝宽度给定的条件下，半角宽度θ与波长成正比。用单色光照射时，波长越长，衍射效应越显著；波长越短，衍射效应变得越不明显。在极限情况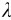→0时，衍射效应可完全忽略。这再一次说明几何光学是短波的极限。

用复色光照射时，由式（10-3）可知，波长不同的单色光的半角宽度不同，其同级的各次级明纹不会重叠在一起。如采用白光照射，除中央明纹为白色明纹外，在其两侧各种单色光按波长自短而长，依次由近到远排成对称的彩色图样。紫色光靠近中央明纹，而红色光则离开中央明纹最远，这种由衍射所产生的彩色图样，称为衍射光谱。

例10-1　在夫琅禾费单缝衍射中：

（1）波长500nm的平行光束垂直入射到缝面，若第一级暗纹对应的衍射角为30°，求窄缝的宽度?

（2）如果单缝的宽度a=0.5mm，在焦距f=1m的透镜的焦平面上观察到衍射条纹中中央明纹有多宽?其他明纹有多宽?

解　（1）由式（10-2）知，第一级暗纹满足条件：

所以单缝宽度

由此可知，要制作如此窄的狭缝，制造工艺较为困难，且透过单缝的能量也太少，条纹强度很弱，不易观察。

（2）当宽度a=0.5mm时，第一暗纹对应的衍射角为θ₁，所以有

由于sinθ₁甚小，故

θ₁≈sinθ₁=10^-3rad（约0.06°）

中央明纹的宽度，即两侧第一暗纹之间的距离。由式（10-4）可得

Δx=2ftanθ₁=2fθ₁=2×10^-3m=2mm

而各次级明纹之间的距离为

中央明纹宽度是其他次级明纹宽度的两倍，其他明纹宽度都相等为1mm。