§9-3　劈尖干涉　牛顿环

如果平行光束入射到不均匀的薄膜上，所产生的干涉将不再是等倾干涉现象。这种情况下，我们会观测到等厚干涉条纹。常见的等厚干涉有劈尖干涉和牛顿环。

一、劈尖干涉

在两块相叠合的平面玻璃片之间，靠近一端处垫入一薄纸片，如图9-12（a）所示，在两玻璃片之间形成一劈尖形空气薄膜，称为空气劈尖。两玻璃片的交线称为棱边，在平行于棱边的线上，对应的空气厚度是相等的。

设平行单色光垂直（i=0）入射到组成劈尖的玻璃片上，在空气劈尖（n₂=1）上、下两表面所引起的反射光将形成相干光，劈尖在C点处的厚度为d，当光线a、b在劈尖表面反射，形成两相干光线a₁、b₁的光程差可用式（9-19）。将i=0，n₂=1代入后，得到a₁、b₁这两条光线之间的光程差为

故反射光的干涉条件为

由式（9-21）可知，每一明、暗条纹都与一定的k值相联系，即与劈尖的一定厚度相对应。因此这些条纹称为等厚干涉条纹。等厚干涉条纹可用透镜或眼睛聚焦在劈尖的表面上观察到。

等厚干涉条纹的形状决定于厚度相同地方的轨迹。在劈尖中，如果玻璃片的表面是严格的几何平面，干涉图样是平行于劈尖棱边的一组明暗相间的平行条纹，如图9-12（b）所示。图中实线表示暗条纹，虚线表示明条纹。

两块玻璃片相接触处d=0，光程差等于2，由式（9-21）应看到暗条纹，而事实上也正是这样。这再次证明光波垂直入射在光密介质表面上反射时，有半波损失。

如图9-12（b）所示，任何两相邻明条纹或暗条纹之间所对应的空气厚度之差为

对于折射率为n的介质劈尖，式（9-20）应有d_k+1-d_k=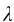/2n。若以光程差表示厚度差，则任何相邻明条纹或暗条纹之间对应的厚度差仍为/2，所以任何两个相邻的明条纹或暗条纹之间的距离由下式决定

式中，θ为劈尖的夹角，显然θ越小，干涉条纹越稀疏；而θ越大，干涉条纹越稠密。如果劈尖的夹角θ相当大，干涉条纹将无法分辨。干涉条纹只能在很薄的劈尖上才能看到。

由式（9-22）可知，如果已知劈尖的夹角θ，测出干涉条纹就可以计算出单色光的波长；如果已知单色光的波长，就可以计算出微小的角度θ。

工程技术上常利用式（9-22）测定细丝的直径或薄片的厚度及检测加工平面的质量。

二、牛顿环

等厚干涉的另一例是牛顿环。如图9-13（a）所示，它是在一块平板玻璃B上，放置一曲率半径R很大的凸透镜A所构成的。在透镜的凸表面与平板玻璃的平面间，形成一个厚度由零逐渐增大，且两表面的夹角也随之增大的空气薄层。在以两表面接触点为中心的圆周上空气层的厚度相等。所以当单色平行光垂直射向平凸透镜时，由透镜下表面所反射的光和平面玻璃板上表面反射的光发生干涉，将呈现干涉条纹。干涉条纹的形状是以接触点O为中心的许多同心环，称为牛顿环，如图9-14所示。牛顿环的明、暗干涉环纹处的空气层厚度d由下述条件决定：

从图9-13（b）看出，圆环半径为r处，空气层厚度d满足关系式：

r₂=R₂-（R-d）²=2Rd-d²(www.daowen.com)

因平凸透镜与平板玻璃间空气层极薄，则有R>>d, d²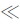2Rd，略去d²项，上式变为

式（9-24）表明，某环纹所在处，空气层的厚度与该处圆环半径r的平方成正比。所以距接触点O越远，光程差增加得越快，环纹也变得越来越密。在接触点O处，d，两反射光的光程差为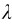/2，因而牛顿环的中心是暗点。

把式（9-24）代入式（9-23），求得反射光干涉的明环和暗环的半径分别为

上述劈尖干涉和牛顿环的干涉图样，都是在薄膜反射光中看到的。在透射光中，同样也可以看到干涉图样；但透射光干涉图样的明暗纹的位置与反射光的明暗纹的位置恰好相反，即在劈尖干涉中，棱边处是明条纹，而在牛顿环中接触点是亮点。

例9-3　折射率n=1.4，夹角θ=10^-4rad的劈尖，在单色光的垂直照射下，测得两相邻明条纹之间的距离l=2.5×10^-3m。求单色光在空气中的波长。

解　在劈尖的表面上，如图9-15所示，取第k条和第k+1条相邻的明条纹，用d_k和d_k+1分别表示两明条纹所在处劈尖的厚度。根据明条纹的条件，d_k和d_k+1应分别满足下列两式：

两式相减，得

由式（9-22）可知，（d_k+1-d_k）与两相邻明条纹的间距l之间的关系为lsinθ=（d_k+1-d_k），因此得

或

将n=1.4，l=2.5×10^-3m，θ=10^-4rad代入，注意到θ很小，即由sinθ≈θ，则得

例9-4　用钠光灯的黄光观察牛顿环现象时，看到第k级暗环的半径r_k=4mm，第k+5级暗环半径r_k=6mm。已知黄光的波长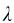=589.3nm，求所用平凸透镜的曲率半径和k级为第几级暗环。

解　根据牛顿环的暗环公式r=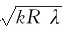，得

从以上两式得

将有关数据代入上式，计算得

R=6. 79m

k=4