§9-2　光程和光程差　薄膜干涉

在杨氏双缝干涉实验中，两束相干光是在同一介质中传播的，它们在相遇处叠加时的相位差，仅决定于两光之间的几何路程之差。一般情况下，无论是人们设计的其他干涉实验，还是自然界中的干涉现象，两束相干光不都是在同一介质中传播。例如，我们即将讨论的薄膜干涉，两束相干光就是经过不同介质产生的干涉现象。两相干光间的位相差不能再单纯由它们的几何路程之差来决定，因此需要介绍光程和光程差的概念。

一、光程和光程差

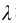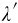实验指出，单色光经过不同介质时，频率恒定不变，它由光源决定。而光速和波长则均随介质的不同而改变。设单色光的频率为ν，c和u分别为给定的单色光在真空中和在介质中的光速，n为该介质的折射率，则有u=c/n。若和分别表示该单色光在真空中和介质中相应的波长，由波速、波长和频率间的关系c=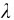和u=ν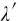，得到介质中的波长为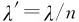，即单色光在介质中的波长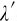是真空中波长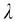的1/n。因此在折射率为n的某一介质中，如果光波在一段时间内通过的几何路程为x，那么在相等的一段时间t内，光波在真空中通过的几何路程即为

这表明光波在介质中的几何路程x，相当于在真空中的几何路程nx。换句话说，光波在介质中传播所经历的路程x，折算到真空中的传播所经历的路程等于nx。在光学中，我们将光波在某介质中几何路程x与该介质的折射率n的乘积nx，定义为光程。引入光程这一概念后，光波在介质中传播的有关问题，都可以折算到光波在真空中传播进行讨论，从而便于我们计算光波在介质中传播时所经历的路程与相位变化间的关系。

设相位相同的两相干光源S₁和S₂发出的相干光波，分别经过折射率n₁和n₂的两种不同的介质在P点相遇，如图9-8所示，两束光在P点的相位差为

式中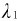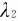，、为光波在两种介质中的波长，r₁、r₂是两束光的几何路程，根据光波在介质中的波长与其在真空中波长的关系，式（9-13）可改写为

上式中，n₁r₁和n₂r₂分别为光波在折射率为n₁和n₂的介质中的光程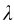，是光波在真空中的波长，二者之间的光程差以Δ表示，则

Δ=n₂r₂-n₁r₁

利用式（9-14）、式（9-13）可进一步改写为

上式表示，两种不同介质中传播的相干光，光程差与其在相遇点处引起的相位差之间的关系，式（9-15）是考虑光的干涉问题时，常用的一个基本关系式。

应强调指出，引进光程后，不论光在什么介质中传播，式（9-15）中的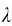都是真空中的波长。此外，如果两相干光源不是同相位的，则还应加上两相干光源的相位差，才是两光束在P点的相位差。于是，采用光程的概念后，两相干光束（从同相点算起）的相干条件便可用光程差直接写出：

在观察干涉、衍射等现象时，经常要用到透镜。不同光线通过透镜可改变传播方向，也会引起附加光程差吗?由几何光学知道，从实物点发出的球面波，经过凸透镜会聚成一个明亮的实像点。这证明从物点到像点各光线经历了相同的相位变化，也就是经历了相同的光程，称为物点到像点各光线的等光程性。如图9-9所示，虽然从物点S到像点S′经历的几何路程不相等，但光程是相等的。

如图9-10（a）所示，一束平行光线平行于透镜主光轴入射，透过透镜后会聚于一点F（焦点），在F点呈现亮点，波阵面上A、B、C各点是同相位的，各光线经过透镜到达F点处也是同相位的，说明从A、B、C各点通过透镜到达F点的光程是相等的。图9-10（b）是一束平行光束平行于透镜的某一副光轴入射，会聚到F点（副焦点），由等相面上A、B、C各点入射到透镜上，各条光线的光程不相等，但通过透镜后到F点时，各光线的光程却是相等的。

综上所述，使用透镜可以改变光线的传播方向，但对光线不会产生附加的光程差。

二、薄膜干涉

光线入射到厚度均匀的透明薄膜上，在薄膜上下表面反射的光在空间相遇所形成的干涉，称为薄膜干涉。如肥皂泡上水面上的油膜在太阳光的照射下呈现出美丽的彩色，就是薄膜干涉现象。

入射到薄膜上的光波，其中一部分被薄膜上表面反射，另一部分透过薄膜上表面进入薄膜，再被其下表面反射。下表面反射的光波，大部分穿过薄膜上表面射到薄膜外。实际上，这是光的强度的分解过程，光的强度与光矢量振幅的平方成正比。所以，这也就是振幅的被分解过程，这种获得相干光的方法称为分振幅法。(www.daowen.com)

设有一透明薄膜MN，如图所示，薄膜的两个表面平行，其厚度为d，折射率为n₂，膜的两边是折射率为n₁的介质，且n₂＞n₁。当光源S发出波长为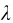的单色光以入射角i入射到薄膜的MN的A点处，入射光的一部分被反射，反射光线为a。大部分入射到薄膜内，其中一部分在下表面C点反射回到B点，然后进入介质n₁为光线b，其余部分由下表面进入介质n₁，在薄膜内的B处也有一部分光反射，由于经过两次反射的光大大减弱，可以忽略不计。光线a、b出自同一光源S，是相干光，当用透镜把它们会聚在焦点P上时，就会产生干涉。

现在我们利用光程差来分析薄膜干涉的加强和减弱条件。光线a所经历的路程为SAP，光线b所经历的路程为SACBP。在图9-11上通过B点作垂直于a和b的线段BD。从图中看出，SA段是a、b两光线共同经历的路程，而DP段和BP段由于通过透镜不附加光程差，则这两段的光程是相等的。所以a、b两光线的光程差为

其中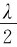，是由于光线入射到薄膜MN上时，在上表面反射有半波损失。从图9-11可以看出：

和

AD=ABsini=2dtanγsini

γ为折射角。根据折射定律n₁sini=n₂sinγ，可得

将AD值及式（9-18）中AC和CB的值代入式（9-17）整理后得

于是决定a和b两反射线会聚点P的明、暗干涉条件为

由上式可以看出，厚度均匀的平面薄膜，光程差是随入射光的入射角i而改变的。如果发散的单色光束照射在厚度均匀的平面薄膜上，相当于每一入射角i都有一束平行光入射，具有相同入射角（相同倾角）的一切光线都有相同的光程差。这样，不同的干涉明条纹或暗条纹，相对应不同的倾角，而同一干涉条纹上的各点都对应相同的倾角，因此这种干涉条纹叫做等倾干涉条纹。

例9-2　垂直入射的白光从肥皂薄膜上反射，在可见光谱中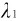，=600nm处有一个干涉极大，而在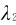=450nm处有一个干涉极小。在这极大与极小之间没有另外的极小，如果膜的折射率n=1.33，问这膜的厚度是多少?

解　对于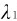=600nm干涉极大，有

对于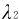=450nm干涉极小，有

根据题意有

k=k′

由以上三式解得

因此得