我们知道，两列频率相同、振动方向相同、相位相同或者相位差保持恒定的波源发射的波，才能发生相互干涉。对于机械波和无线电波，上述条件还比较容易实现，但是对于光波而言，即使发光体（光源）的强度、形状、大小完全相同，甚至频率也相同，干涉条件也仍然不能满足，其原因是由于物质发光机制的复杂性所致。

一、光源

发光体称为光源。按光的激发方式，可把光源分成各种不同的类型。常用的光源有普通光源和激光光源两类，普通光源有热光源（由热能激发，如白炽灯、太阳）和冷光源（由化学能、电能或光能激发，如日光灯、气体放电管）。激发方式不同的光源，辐射机制也不相同。在热光源中，大量分子和原子在热能激发下，从正常态跃迁到高能量的激发态，然后它们自发地从激发态返回低能量的正常态时，以光波的形式将多余的能量辐射出来，这就是光源所发的光。

光源发射光波是一种量子随机过程，各个分子或原子在不同时刻发射的光波频率、振动方向和相位彼此毫无联系，而且分子或原子发光是间歇性的，每次发光时间约为10-8s。我们把分子或原子每次发出的一段有限长、振动方向一定、频率一定、振幅基本不变或变化缓慢的光波称为波列。因为分子或原子发射的各个波列之间，在频率、振动方向和相位等方面没有联系，因此两个独立的光源，同一光源的不同部分，乃至光源同一部分在不同时刻发出的光，在空间某一点叠加时，都不会满足相干条件。

二、光的相干性

1.光的强度

实验表明，人眼和感光仪器所检测到的光的强弱正比于光矢量振幅E₀的平方，所以光的强度

I∝E²₀

通常我们关心的是光强度的相对分布，上式中比例系数可取为1，则光传播的空间内任一点光的强度，可用该点光矢量振幅的平方表示，即

I=E²₀

设两个频率相同，光矢量E方向相同的光源，所发出的光振幅和光强分别为E₁₀、E₂₀和I₁、I₂，它们在空间某处P相遇，P点合成光矢量的振幅E、光强I可分别表示为

E²=E²₁₀+E²₂₀+2E₁₀E₂₀cosΔφ

式中，Δφ为两光振动在P点的相位差，由于分子或原子每次发光持续时间极短（约为10-8s），我们所观察到的光强是在一个波动周期T内的平均值，即

2.非相干叠加

由于分子或原子发光的间歇性和随机性，在T时间内，在叠加处随着光波列的大量更替，来自两个独立光源的两束光，或同一光源的不同部位所发的光的相位差Δφ随时间变化，它可取0到2π之间的一切数值，且概率相等，因而cosΔφ对时间的平均值为零，则有

I=I₁+I₂

上式表明，两个独立光源，或同一光源不同部分发出的光，叠加后的光强等于两束光单独照射时的光强I₁和I₂之和，观察不到干涉现象，式（9-5）称为非相干叠加强度公式。

3.相干叠加

如果利用一定的方法，获得满足频率相同、振动方向相同、相位差恒定的相干条件的两束相干光，在空间的P点相遇合成后的光强为

因相位差恒定，故在P点的光强始终不变，对于两波相遇区域的不同位置，其光强由两光束在这些位置的相位差决定，即空间各处光强分布将由干涉项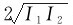cosΔφ决定，在一些地方始终加强，另一些地方始终减弱；若有I₁=I₂，则合成后的光强为

当Δφ=±2kπ时，这些地方的光强最大（I=4I₁），称为干涉相长，即亮纹中心；当Δφ=±（2k+1）π时，这些位置的光强最小（I=0），称为干涉相消，即暗纹中心。光强I随相位差变化情况如图9-1所示。

综上所述，只有两束相干光叠加才能产生干涉现象。而获得相干光，只有将同一发光原子或分子每次发出的波列均分成两束，才可能满足相干条件，因为这样的两束光频率和初相位必然完全相同，在空间相遇点的相位差恒定，并且振动方向也相同，从而满足相干条件。

三、杨氏双缝干涉实验

1801年英国物理学家托马斯·杨（T.Young）巧妙地实现了光的干涉，观察到了光的干涉现象。实验装置如图9-2所示，一束太阳光入射到带小孔S的屏上，S可以视为点光源，从S发出的球面波遇到其后面开有两个小针孔S₁和S₂的屏。S₁和S₂的光振动都来自同一点光源S，是由同一波振面分出来的，满足相干条件。从S₁和S₂发出的光波到达后面的接收屏E上，就得到明暗相间的干涉图样。S₁和S₂即为一对相干光源，这种获得相干光源的方法称为分波阵面法。后人为了提高干涉图样的清晰程度，用单色光代替复色光，把小孔改为狭缝，从而构成了平时所说的杨氏双缝干涉实验。双缝干涉条纹的明暗对比度十分明显，干涉条纹都与狭缝平行，条纹间距相等。

总结其实验结果：

（1）干涉条纹是以图9-2中与S₁及S₂等距离的P₀为对称点，明暗相间分布，P₀处是中央明条纹。(www.daowen.com)

（2）用不同的单色光源做实验时，各明暗条纹的间距并不相同，波长较短的单色光，如紫光，条纹较密集；波长较长的单色光，如红光，条纹较稀疏。如图9-3所示。

（3）如用白光复色光做实验，在屏E上只有中央条纹是白色的，在中央白色条纹两侧，由于各单色光的明、暗条纹的位置不同，形成由紫至红的彩色条纹。

下面我们对双缝干涉作定量分析。在屏E上，出现的明、暗条纹是由强度分布决定的，当相干光源S₁及S₂发出的光波在屏E上P点相遇时，P点的光强由式（9-6a）知

式中，Δφ为两束光波在P点的相位差。由于S₁、S₂发出光波的初相位相同，从而

式中，r₁、r₂分别是S₁、S₂到P点的距离，如图所示。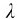为单色光波长，δ=r₁-r₂是光波分别从S₁、S₂传播到P点的波程差。当

于是有

即P点到双缝的波程差为波长的整数倍时，P点处将出现明条纹，其中k称为干涉级，k=0的明条纹称为零级明纹或中央明纹，k=1，2，……对应的明纹，依次对称的分布在中央明纹两边，分别称为第一级明纹，第二级明纹……；若P点到双缝的波程差为半波长的奇数倍时，P点出现暗条纹，k=0，1，2，……对应的暗纹对称分布于中央明纹两边，分别称为第一级暗纹、第二级暗纹……。波程差为其他值的各点，光强介于明暗纹之间。

图9-4中，N₁和N₂分别为S₁和S₂在屏E上的投影点，O为N₁和N₂的中点，并设OP=x，则P点到S₁和S₂的距离r₁和r₂分别由下面两式给出：

式中，D为双缝和屏之间的距离，a为双缝之间的距离。因D>>a，可取r₁+r₂=2D，不难推得

即有

将式（9-10）代入式（9-9），得

由式（9-11）可知，相邻两明条纹或两暗条纹间的距离为

因此干涉条纹是等距离分布的。但是由于条纹间距Δx与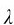成正比，波长不同的单色光条纹间距并不相等。由此不难理解图9-3中随波长不同，相应条纹分布稀疏、密集的情况。当用白光作光源时，在中央P₀处是白色的条纹，其余的各级都是由紫而红的彩色条纹，如图9-5所示。随着级数的增大，紫色和红色间的距离拉宽，不同级的条纹互相重叠，使条纹越来越模糊。

根据光的波动理论，我们比较圆满地解释了双缝干涉的实验结果。杨氏双缝干涉实验不但为19世纪初确认光的波动说和此后建立光的波动理论提供了实验基础，而且人们利用双缝干涉首次测定了光的波长。其具体方法是对于待测光波的干涉图样，测量出相邻明条纹或暗条纹间的距离，利用式（9-12）便可求出光波的波长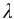。上述事实奠定了杨氏干涉实验在光学发展史中的重要地位。

例9-1　在双缝干涉实验中，双缝间距a，缝与屏幕的距离D，测得第个明条纹的位置x。问光源的波长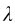是多大?

解　根据明条纹公式得

四、菲涅耳双镜和劳埃镜

杨氏双缝实验之后，菲涅耳（A.J.Fresnel）、劳埃（H.L.Loyd）也同样以分波振面法获得相干光源，分别用双镜和劳埃镜的实验装置实现了光的干涉，简述如下。

1.菲涅耳双镜

如图9-6所示，一对紧靠在一起夹角很小的平面镜M1和M2，构成菲涅耳双镜。狭缝光源S与两镜面的交棱C平行，于是从光源S发出的光经M1和M2反射后成为两束相干光，在它们重叠区域内的屏E上将会出现等距的平行干涉条纹。

设S₁和S₂为S对M₁和M₂所成的两个虚像，则屏E上的干涉条纹，就如同是由相干的虚光源S₁和S₂发出的光波所产生的一样。因此，可利用杨氏双缝干涉的结果计算该实验中的明暗条纹的位置及间距等。

2.劳埃镜

图9-7给出了劳埃镜实验示意图，劳埃镜是一块下表面涂黑的平面玻璃片或金属板。从狭缝S₁发出的光，一部分直接射向屏E，另一部分以近90°的入射角掠射到镜面MN上，然后反射到屏E上。S₂是S₁在镜中的虚像，反射光可看成是虚光源S₂发出的，它和S₁构成一对相干光源，于是在叠加区内的屏上出现明、暗相间的等距离干涉条纹。

若将屏E移至镜端N处且与镜接触，则在接触处屏E′上出现的是暗条纹，该处距S₁和S₂的波程相等，应该出现明条纹。这表明由S₁直射到屏上的光波和从平面镜反射来的光波之间有一相位π的突变。这意味着光从光疏介质（折射率较小的介质）掠射向光密介质（折射率较大的介质）的界面反射时，损失了半个波长的波程，这种现象称为半波损失。实验表明，光从光疏介质入射到光密介质而被反射时，都会产生半波损失，故在计算光程时要特别注意将其计算在内。