§8-5　多普勒效应

前面所讨论的波动实际上假定了波源和观察者相对于介质是静止的情况，所以观察者接收到的波的频率与波源的振动频率相等。但在日常生活和科学技术中经常遇到波源或观察者相对介质运动的情况。如我们站在铁路旁，高速行驶的火车鸣笛而来时听到汽笛的音调变高，即频率变大；火车鸣笛而去时听到汽笛的音调变低，即频率变小。这种因波源或观察者相对于介质运动，而使观察者接收到的波的频率发生变化的现象称为多普勒效应。

为了讨论简单，选介质为参考系，并假定波源和观察者的运动发生在两者的连线上，分别用v_S和v_B表示波源和观察者相对于介质的运动速度，u表示波在介质中的传播速度。并规定：波源和观察者向对方接近时v_S、v_B取正值，向对方远离时取负值。此外还要区别波源频率、波的频率和观察者接收到的频率。波源在单位时间内振动的次数，称为波源的频率，用v_S表示；波传播时介质中质点在单位时间内振动的次数，称波的频率以ν表示；观察者在单位时间内接收到波的振动次数，为观察者接收到的频率，用ν_B表示。由于波速只决定于介质的性质，而与波源和观察者的相对运动无关，它恒为正值。波在介质中的波长为，则u=ν。

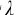一、波源不动　观察者以速度υ_B相对介质运动

若观察者向波源运动，如图8-14所示，如果观察者在P点不动，波在单位时间内向右通过P点传播了u的距离，观察者接收到的完整波数，即为分布在距离u中的波数。当观察者以速度υ_B向波源运动，在单位时间内观察者向左移动了υ_B的距离。在单位时间内观察者接收到的完整波数，应该是距离υ_B+u中的总波数，即

由于波源相对介质静止，所以波的频率ν等于波源的频率ν_S，则上式可表示为

式（8-24）表明当观察者向着波源运动时，观察者接收到的频率变高了，为波源频率的1+倍。而当观察者远离波源运动时，通过上述类似地分析，可知观察者接收到的频率为

二、观察者不动波源以速度vS相对介质运动

如图8-15所示，波源向观察者运动，在运动中波源仍按照自己的频率发射波。波长是介质中波线上相位差为2π的两个相邻的振动状态相同的两点之间的距离。在一个周期内波在介质内传播了距离uT_S，完成了一个完整的波形，即波源在S₁发出的某一振动状态，经过一个周期的时间已传到位置A。而与此同时波源已由位置S₁移动了距离υ_ST_S到达S₂，并发出相位差为2π的另一振动状态。结果使一个完整的波形被挤压在S₂A之间，这相当于波长减小为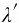=uT_S-υ_ST_S。因此观察者在单位时间接收到的完整波的数目，即观察者接收到的频率为(www.daowen.com)

此时观察者接收到的频率大于波源频率。

当波源远离观察者运动时，则可求得观察者接收到的频率为

此时观察者接收到的频率小于波源的频率。

三、波源与观察者同时相对介质运动

根据前面的讨论可知，观察者以υ_B相对介质运动时，相对观察者来说，波的速度变为u′=u+υ_B；而波源以υ_S相对介质运动时，相当于使波长变为=uT_S-υ_ST_S。综合这两个结果，则波源与观察者相向运动时，观察者接收到的频率为

当波源和观察者彼此离开时，观察者接收到的频率为

由式（8-28）和（8-29）可见，不管是波源运动还是观察者运动，或者两者同时运动，只要观察者和波源相互接近，观察者接收到的频率就高于波源的频率；而只要两者相互远离，观察者接收到的频率就低于波源的频率。

多普勒效应也是波动过程的共同特征，不仅机械波有多普勒效应，电磁波也有多普勒效应。不过因为电磁波可以在真空中传播不需要介质。相应地，在电磁波的多普勒效应中，由光源和观察者的相对速度来决定观察者的接收频率。多普勒效应在光学应用中的一个重要例子：当光源远离观察者运动时，接收到的频率变小，波长变长。这种现象称为红移，即移向光谱中的红色一侧。多普勒效应在科学技术中有广泛应用。例如，利用星球的光谱与地球上相同元素的光谱间的红移现象，证明星球都在远离地球而运动，从而为所谓宇宙“大爆炸”理论提供了重要证据。此外利用声波的多普勒效应可监测车辆的速度和测量水下潜艇的速度；医学上利用超声波的多普勒效应来诊断心脏的跳动情况等。