§8-4　惠更斯原理　波的叠加原理

一、惠更斯原理

波动的起源是波源的振动，波的传播是由于介质质点之间的弹性相互作用。介质中任一点的振动将直接引起邻近各质点的振动。所以在波动中介质中任何一质点都可以看做是新的波源，如图8-7所示，一列波在前进中遇到一障碍物AB, AB上有一小孔，孔径a比波长小很多，这时可以看到：通过小孔的波是以小孔为中心的新的球面波，与小孔前的波形无关，说明小孔可视为新的波源。

1690年惠更斯总结了上述这类现象，他提出：介质中波前（波阵面）上的各点，都可以看做是发射子波的波源。其后任一时刻这些子波的包迹就是新的波前，这就是惠更斯原理。惠更斯原理不但对机械波适用，对电磁波和各种波动过程都适用。根据这一原理，用几何作图的方法，可方便地决定下一时刻的波前，从而在很广泛的范围内解决了波的传播问题。下面以平面波和球面波为例说明惠更斯原理的应用。

点波源O在各向同性的均匀介质中，以波速u发出球面波。已知t时刻传播到半径为R1的球面波前S₁，以S₁上各点作为发射子波的波源，经过Δt时间后每个子波源向外发射的次级球面波的半径将是uΔt，由这许许多多子波形成的半球面，画出它们的包迹面就得到t+Δt时刻新的波前S₂，显然包迹面S₂的半径为R₂=u（t+Δt）的球面，如图8-8所示。

对于平面波，只要知道某一时刻的平面波前S1，用惠更斯原理也可以作下一时刻的波前S₂，如图8-9所示。

二、波的叠加原理

在音乐会上欣赏乐队伴奏的男女二重唱时，我们可以分辨出各种乐器和男女各自的声音。说明各种乐器和男女各人发出的声波，并不受其他乐器或人发出的声波的影响。即一列波的振幅、频率、振动方向以及传播方向等，都不因别的列波存在而发生改变。由此可见介质中的每一列波都保持其独立的传播特性。当有几个波源所产生的波同时在介质中传播，并在某点相遇时，相遇处质点的振动将是各列波单独存在时引起的分振动的合成。对机械波而言，n列波在空间某处相遇时，相遇处质点振动的位移就是各列波单独存在时在该点引起的位移的矢量和，如图8-10所示。通过实验观测到的关于波动现象的这一结论，概括为波的叠加原理，或称波传播的独立性原理。

三、波的干涉

根据波的叠加原理定量地分析波的叠加情况，任意几列波叠加时合成波一般比较复杂且不稳定，没有实际意义。但满足特定条件的两列波在介质中相遇，可形成一种稳定叠加图像。如果频率相同、振动方向相同、相位相同或相位差恒定的两列波在空间传播相遇时，叠加区域内出现某些点的振动始终加强，另一些点的振动状态始终减弱的稳定分布。这种现象谓之波的干涉现象。两频率相同、振动方向相同、相位相同或相位差恒定称为相干条件。满足相干条件的波称为相干波，其相应的波源称为相干波源。

设点波源为S，在S的前边放一开有小孔S₁、S₂的屏，S₁、S₂相对于S对称设置，如图8-11所示。根据惠更斯原理，S₁、S₂可看成两个相位相同的相干子波源，图中用实线代表它们发出的球面波的波峰，虚线代表波谷，它们的波峰或波谷相遇处振动彼此加强，合振幅最大；而在其波峰与波谷相遇处振动彼此抵消，合振幅最小；在其他位置合振动的振幅介于两者之间，但各处振幅均不随时间发生变化。于是在空间形成稳定的干涉图像。

设两列相干波在P点相遇，如图8-12所示，相干波源S₁和S₂到P点的距离分别为r₁和r₂，设波源S₁、S₂的振动表达式分别为

y₁₀=A₁₀cos（ωt+φ₁）

y₂₀=A₂₀cos（ωt+φ₂）

A₁₀和A₂₀分别表示波源S₁、S₂的振幅；φ₁、φ₂表示它们各自的初相位。若这两列波在同一介质中传播，则其波速相同，波长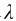也相同。波源的振动传至P点，振幅分别为A₁和A₂，引起的分振动分别为

这是两个同方向、同频率、有恒定相位差的谐振动，其相位差为

根据叠加原理，P点的合振动为

y=y₁+y₂=Acos（ωt+φ）

式中

由式（8-18）可知，满足条件：

的各点，合振动振幅最大，其值为A=A₁+A₂，称为相长干涉；而满足

的各点，合振幅最小，其值A=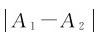，称为相消干涉。

如果两相干波初相位相同，即φ₁=φ₂，则式（8-18）可简化为

若再令r₁-r₂=δ，δ表示从两相干波源S₁、S₂分别到达P点所经历的路程之差，称为波程差。于是有(www.daowen.com)

上式给出了相位差与波程差的关系。引入波程差的概念之后，干涉加强、减弱的条件简化为

上式表明，当两个相干波源同相位时，在两列波叠加区域内，在波程差等于零或波长的整数倍的空间各点，合振动的振幅最大；而波程差等于半波长的奇数倍的空间各点合振动的振幅最小；波程差为其他值时，合振动的振幅介于A₁+A₂和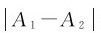之间。

应强调指出，干涉现象是波动过程的基本特征之一，对干涉现象的研究不但对光学、声学是重要的，而且在现代物理学的发展和应用技术上也极为重要。

例8-3　在图8-13中，A、B为同一介质里两个同振幅的相干波源，A、B相距20m，频率均为100Hz，波速为200m/s，且A点为波峰时，B点恰好为波谷。求AB连线之间因干涉而静止的各点位置?

解　解法一：

根据题意，先写出波源的振动方程，然后再由波的表达式，找出它们在AB连线上某点C的合振动方程，最后根据干涉条件，求出振幅为零的点的位置。A点的振动方程为

y_A=Acosωt

由于A、B相位相反，B的振动方程为

y_B=Acos（ωt+π）

设任意点C距波源A的距离为x，即BC=AB-x=20-x，则波源A在C点引起的分振动方程为

波源B在C点引起的分振动方程为

因干涉而静止应满足条件：

化简为

将已知数据代入，得

x=10+k（k=0，±1，±2，……±9）

所以AB连线上因干涉而静止的各点，在距A为1m、2m、3m、……19m的各点。

解法二：

直接利用相位差表示的干涉相消条件

（k=0，±1，±2，……）

由题意知φ₂-φ₁=π，若r₁=x，则r₂=20-x，由波速公式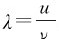，所以有

化简得

x=10+k（k=0，±1，±2，……±9）