§8-3　波的能量

一、波的能量和能量密度

波动在传播过程中，介质中的各质点依次投入振动，故有振动动能，同时因发生形变而具有弹性势能。所以，机械波的能量就是介质中各质点振动的动能和势能的总和，并且波的能量伴随波的传播具有由近及远传播开来的特性。

我们以弦线上传播的横波为例，讨论波的能量变化规律。如图8-5所示弦线上取一线元Δx，其质量为mΔx，振动速度为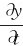，因此其动能为

式中，m为弦线单位长度的质量。

可以证明，由于介质形变，线元Δx的势能与动能相等，即

ΔE_k=ΔE_p

上式表明任一时刻介质中介质元动能和势能都相等，同时达到最大值或最小值。这与孤立质点时能量守恒不同。

对于简谐波线元的总能量为

式（8-9）表明波动能量分布在弦线上各线段内。弦线单位长度的能量，即能量密度，正比于振幅的平方和圆频率的平方，并且随着波的传播按正弦函数的平方作周期性地变化。

三维空间传播的波，能量将分布在体积ΔV内，体积元的质量ρΔV，ρ为介质的密度，所以简谐波能量的一般表示为

为了描述介质中能量的分布情况，引入能量密度，即单位体积中的能量，用W表示，即

容易看出能量密度W的变化周期为波动周期的一半，T′=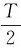=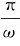。能量密度在一个周期T′=中的平均值，称为平均能量密度，有

由式（8-12）可知，波的能量与振幅的平方以及介质密度成正比。式（8-12）适用于所有弹性介质的行波。(www.daowen.com)

二、能流密度

波动过程实际上就是能量的传播过程。能量来自波源，通过介质中各质点的振动耦合，每个质点都不断地接收能量，同时向后边质点传递能量。能量传播的方向也就是波的传播方向，能量的传播速度等于波速。

为了描述波动过程中能量的传播，引入能流的概念，把单位时间内通过介质中某一截面的能量叫做通过该截面的能流。设想在介质中取一垂直于波速u的截面ΔS，单位时间内通过截面ΔS的能量恰好等于底面为ΔS、垂直ΔS的边长为u的柱体内的平均能量，如图8-6所示。所以通过截面ΔS的平均能流为

通过垂直于波的传播方向单位面积的平均能流称为能流密度，用I表示：

能流密度I的大小与介质的密度、波速、振幅平方和圆频率的平方成正比。能流密度越大，单位时间内通过与波速垂直的单位面积的能量越多，它决定了波的强弱。因此能流密度也称为波的强度。能量的传播方向与波速方向一致，能流密度也反映了能量传播的快慢和方向。把它写成矢量形式

在SI单位制中，能流密度的单位为W/m²。

例8-2　在介质不吸收能量的情况下，一点波源向外发射球面波。求距波源为r1、r2两处的能流密度之比和振幅之比?

解　设距波源为r₁、r₂两处的能流密度分别为I₁、I₂，振幅分别为A₁、A₂。以波源为中心，以r₁、r₂为半径分别作两个同心球面。由于介质不吸收能量，根据能量守恒定律，波传到半径为r₁的球面的平均能流等于波传到半径r₂的球面的平均能流，即有

I₁·（4πr1²）=I₂·（4πr2²）

从而得

将式（8-14）代入式（8-16），化简得

即球面波的振幅A与离开波源的距离r成反比。