§8-2　平面简谐波

波源和介质中各点均做简谐振动时，形成简谐波。如果简谐波在空间的波面是一系列平行平面，则称为平面简谐波。任何复杂形式的波都可以分解成若干个不同频率的平面简谐波，平面简谐波是最基本的波动形式。如同简谐振动一样，平面简谐波也是一种理想模型。

设在无限大均匀、无吸收的理想介质中，有一平面简谐波沿x轴正向传播，波速为u，如图8-4所示。平面简谐波沿x轴传播，x轴为一波线。现讨论波线上各质点的振动规律。取波线的始点为波源点，且为坐标原点。则原点O处质点的振动规律为

y₀=Acos（ωt+φ）

式中，y0是位于原点O处的质点t时刻的位移，A为振幅，ω为圆频率，φ为初相。波动过程中，质点的振动相位以速度u沿x轴向前传播。考察x轴上任意点P，设OP=x，则原点O处的振动相位传到P点所需时间为Δt=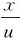，P点的振动相位落后于原点的相位。原点t时刻的相位（ωt+φ），要经过Δt=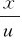时间才能传到P点，即P点t时刻的振动相位和t-Δt时刻原点处质点的相位相同。因此P点处质点在t时刻的振动方程为

因为P点是波线上的任意点，去掉脚标写成一般形式：

式中，振幅A是常量，描述的是介质不吸收的理想情况。式（8-4）给出了以速度u沿x轴正向传播的平面简谐波的一般表达式，平常也称为平面简谐波的波动方程。一般情况下坐标原点并不一定选在波源点上，此时式（8-4）所描述的波动过程，不再限于原点右侧，而是波动沿x轴自左向右的传播。

当y与x垂直时式（8-4）描述的是横波；若y与x轴一致，式（8-4）则表示纵波。x是波线上任一质点平衡位置的坐标；而y是质点离开平衡位置的位移，它是x和t两个变量的函数。考虑到ω、ν、T、u和各量间的关系，式（8-4）可以有如下形式：

另外，当波沿x轴负方向传播时，原点右侧波线上任意点的相位，将比原点超前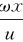，其波的表达式为

例8-1　平面简谐波的波长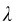=10m，在波的传播方向上某点P的振动方程y=2cos8πt。求：

（1）波的周期和传播速度；(www.daowen.com)

（2）以P点为原点并向右传播写出波的表达式；

（3）坐标为-6m和8m的两点M、N的振动方程及其相位差。

解　（1）由P点的振动方程

y=2cos8πt

可知ω=8π，波的周期：

传播速度：

（2）以P点为原点波的表达式为

（3）将M点的坐标x=-6m和N点的坐标x=8m分别代入波的表达式，可得M点的振动方程为

N点的振动方程为

M、N点的相位差为