§7-3　简谐振动的合成

振动的合成是自然界中普遍存在的现象，例如，人们听到的交响乐声或其他多个声源同时发来的声音，都是振动合成的结果。在数学上，任一周期函数均可展开为由正弦和余弦函数所表达的傅立叶级数。所以，一切振动的合成均可归结为简谐振动的合成问题。

一、同方向、同频率简谐振动的合成

设某质点同时参与两个同方向、同频率的简谐振动

x₁=A₁cos（ωt+φ₁）

x₂=A₂cos（ωt+φ₂）

根据运动的叠加原理，则质点的合位移为

x=x₁+x₂=A₁cos（ωt+φ₁）+A₂cos（ωt+φ₂）

=（A₁cosφ₁+A₂cosφ₂）cosωt+（A1sinφ₁+A₂sinφ₂）sinωt

上式可化简为

x=Acos（ωt+φ）

可见，两分振动的合成运动为与分振动同频率、同方向的简谐振动。其中合振动的振幅A和初相φ分别为

以上为进行三角函数运算的解析法。利用旋转矢量也可更直观方便地讨论上述的合成问题。

如图7-8所示，当两分振动的旋转矢量分别为A₁和A₂时，它们与x轴的夹角分别为φ₁和φ₂；在x轴上的投影分别为x₁和x₂。合矢量A=A₁+A₂为平行四边形的对角线。由于A₁、A₂以相同的角速度逆时针转，它们的夹角（φ₂-φ₁）保持不变。所以矢量A的大小也保持不变，并以相同的角速度ω逆时针旋转。由图7-8可以看出，在任一时刻t，在x轴上的投影为

x=x₁+x₂=Acos（ωt+φ）

式中的初相φ等于t=0时A与x轴的夹角。由此表明，合振动仍为与分振动同方向、同频率的简谐振动，合矢量A即为合振动所对应的旋转矢量。由图7-8可得(www.daowen.com)

Acosφ=A₁cosφ₁+A₂cosφ₂

Asinφ=A₁sinφ₁+A₂sinφ₂

由此可得式（7-15）、式（7-16）两式。

由式（7-15）可知，合振动的振幅A与两分振动的相位差（φ₂-φ₁）有关。当φ₂-φ₁=±2kπ（k=0，1，2，……）时，A=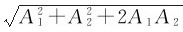=A₁+A₂，即合振幅等于两分振幅之和，为最大值；当φ-φ=±（2k+1）π（k=0，1，2，……）时，A=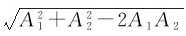=，即合振幅等于两分振幅之差的绝对值，为最小值。其他情况的合振幅均介于二者之间。

二、同方向、不同频率简谐振动的合成

当两个同方向、不同频率的简谐振动合成时，由于它们的相位差随着时间不断变化，合成振动的情况比较复杂，一般不再是简谐振动。但当两简谐振动的频率之差比其频率之和小得很多时，将会呈现出“拍”的特殊现象。为了突出讨论由于频率不同引起的效果，特设两分振动的振幅A及初相φ都相等，而角频率分别为ω₁和ω₂，即

x₁=Acos（ω₁t+φ）

x₂=Acos（ω₂t+φ）

则合振动t时刻的位移为

x=x₁+x₂=A[cos（ω₁t+φ）+cos（ω₂t+φ）]

利用三角函数关系可求得

由于，所以式（7-17）所表示的运动可看做是振幅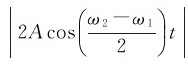缓慢变化，角频率为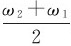的特殊简谐振动。这是振幅有周期性变化的“简谐振动”，如图7-9所示。这种振幅时大时小的现象称为“拍”，合振幅每变化一个周期叫做一拍，单位时间内拍出现的次数，即合振幅变化的频率，称为拍频。由于振幅只能取正值，因此拍2A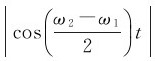的频率为其绝对值频率的2倍，故有

即拍频率等于两个分振动频率之差。

拍现象在声振动、电磁振荡中经常遇到。例如，利用拍现象测定振动频率、校正乐器和制造拍振荡器等。