§7-2　简谐振动的能量

现在仍以弹簧振子为例讨论简谐振动的能量。在振动过程中，由于物体的运动和弹簧的形变，所以振动系统既有动能，又有势能。设振子质量为m，弹簧的劲度系数为k，在某一时刻t，物体的位移和速度分别为x和v，由式（7-3）、式（7-4）知

x=Acos（ωt+φ）

v=-ωAsin（ωt+φ）

于是在t时刻振动系统的动能和势能分别为

这表明系统的动能和势能是按正弦或余弦函数的平方作周期性的变化。其变化的周期为简谐振动周期的一半。图7-7所示为初相φ=0时的简谐振动曲线和动能、势能及总能量随时间的变化曲线。t=0时，位移有最大值A，速度为零，动能为零，故势能最大；t=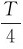时位移为零，速度为-ωA，其绝对值最大，势能为零，动能最大；t=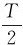时，位移为-A，速度为零，故势能最大，动能为零……

将式（7-10）、式（7-11）相加可得振动系统的总能量为

由此表明，弹簧振子在振动过程中其总能量保持不变，且与振幅的平方成正比。由于在振动过程中只有弹性力做功，只发生动能和势能之间的相互转化，而二者之和的总能量保持恒定不变。由于

所以有

即动能和势能在一个周期内的平均值相等，且等于总能量的一半。

例7-4　一弹簧振子的振动方程为x=Acos（ωπ+φ），其中x的单位为m, t的单位为s。设弹簧的劲度系数为k。求：

（1）当x=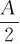时，系统的动能和势能；

（2）物体在什么位置时系统的动能和势能相等。

解　（1）对弹簧振子，系统的总能量为

当x=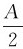时，系统的势能为

所以系统的动能为

（2）设物体在x₀处时系统的动能和势能相等，则有(www.daowen.com)

所以

例7-5　质量为0.1kg的物体，以振幅1.0×10^-2m做简谐振动，其最大加速度为4.0m/s²。求：

（1）振动的周期；

（2）通过平衡位置时的动能；

（3）总能量；

（4）物体在何处其动能和势能相等?

解　（1）因a_max=Aω²，所以有

故

（2）因通过平衡位置时的速度为最大，故

将已知数据代入，得

E_{k, max}=2.0×10^-3J

（3）总能量E=E_{k, max}=2.0×10^-3J

（4）当E_k=E_p时，E_p=1.0×10^-3J，由E_p=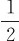kx²=mω²x²，得

即

x=±0.707cm