一、简谐振动

如图7-1所示，把轻弹簧（质量可忽略不计）的一端固定，另一端系一质量为m的物体，放置在光滑的水平面上。若将物体移动后释放，在以后的运动过程中，因阻力可以忽略不计，物体仅受弹簧产生的弹性力的作用，这种由弹簧和物体构成的振动系统称为弹簧振子。当弹簧为原长时，物体受力为零，此时物体的位置为平衡位置O。物体相对平衡位置的位移即为弹簧形变量。取平衡位置O为坐标原点，沿振动线水平向右为x轴的正方向，则当物体相对平衡位置O的位移为x时，由胡克定律知，物体受弹性力为

F=-kx

式中，常数k为弹簧的劲度系数，负号表示力F与位移x的方向相反，即力指向平衡位置。

在该坐标系中，加速度a=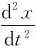，由牛顿第二定律

即

对于给定的弹簧振子，k和m都是正值常量，故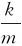可用另一常数ω的平方代替，即

代入式（7-1）可得

该式为二阶线性常微分方程，其解为

x=Acos（ωt+φ）

式中，A、ω、φ均为常量。式（7-3）所表达的振动称为简谐振动，式（7-1）为其动力学方程。凡其动力学方程可归结为式（7-1）的形式的力学系统，其运动则为简谐振动。

将式（7-3）分别对时间求一阶、二阶导数，则可得做简谐振动物体的速度和加速度，即

由此可见，物体做简谐振动时，其位移、速度和加速度都作周期性的变化，且其周期相同。它们与时间的关系曲线如图7-2所示。

二、描述简谐振动的三个参量

1.振幅

在简谐振动方程x=Acos（ωt+φ）中，由于cos（ωt+φ）的最大绝对值为1，所以，位移x的最大绝对值为A。我们把物体离开平衡位置的位移的最大绝对值A称为振幅。

2.周期、频率

物体做一次全振动所经历的时间称为振动周期，用T表示。这就是说，从任意时刻t开始，经过一个周期T后，物体将回到t时刻所处的位置，即

x=Acos（ωt+φ）=Acos[ω（t+T）+φ]=Acos（ωt+φ+ωT）

由于

Acos（ωt+φ）=Acos[ωt+φ+2π]

比较上两式可知

对于弹簧振子，由ω=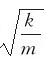，于是有

单位时间内物体完成全振动的次数称为振动的频率，用ν表示。频率的单位为赫兹（Hz），它和周期成倒数关系，即

式中，ω为圆频率（或称角频率），m和k分别为弹簧振子的质量和劲度系数，它是表达振动系统本身的物理性质。由此表明，上述振动系统的振动周期和频率是由振动系统本身的固有性质所决定的。这样的周期和频率称为固有周期和固有频率。

3.相位、初相位

我们知道，物体的运动状态是由位置和速度来描述的。由式（7-3）和（7-4）知，当振幅A和角频率ω一定时，振动的物体在任一时刻相对平衡位置的位移x及其运动速度v都决定于物理量（ωt+φ）。即物体所处的振动状态是由（ωt+φ）决定的。物理量（ωt+φ）称为振动的相位。例如，当相位（ωt₁+φ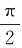）=时，x=0，v=-ωA，此时物体在平衡位置以速率ωA向x轴负方向运动。而当相位（ωt₂+φ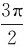）=时，x=0，v=ωA，此时物体在平衡位置以速率ωA向x轴正方向运动。可见，在t₁和t₂两时刻振动的相位不同，物体的振动状态就不同。当t=0时，相位（ωt+φ）=φ，故称φ为初相位，简称初相。它是决定初始时刻物体运动状态的物理量。

4.振幅A和初相φ的确定

简谐振动方程的一般形式为x=Acos（ωt+φ）。式中的A、ω、φ为三个重要常量。对于任何一个具体的简谐振动，它们都有具体的量值。而它们的量值与哪些因素相关?怎样来确定呢?关于角频率ω已在前面阐明，即它是由振动系统本身的性质决定的。下面再来说明振幅A和初相φ怎样确定。由式（7-3）和（7-4）可知，当t=0时有

x₀=Acosφ

v₀=-ωAsinφ

由此两式联立可解得

式中，x₀、v₀为t=0时振动物体的位移和速度，称为初始条件。对于给定的弹簧振子，ω是确定的，由式（7-8）和（7-9）可知，振动系统的振幅A和初相φ是由初始条件决定的。

例7-1　如图7-3所示，劲度系数为k的轻弹簧上端固定，下端系一质量为m的物体，并将物体自平衡位置再拉长x₀后由静止释放并开始计时。问释放后物体的运动是否为简谐振动?若是，则写出其振动方程。

解　设平衡时弹簧伸长l，则有

mg=kl

建立以平衡位置为原点的坐标系，如图7-3所示，则当物体在任一位置x时，物体受合力为

F=mg-k（l+x）=-kx

故有

取ω²=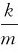则有

所以，物体做简谐振动。

由题意知，t=0时，x=x₀，υ₀=0，故有

由于x₀为正值，υ₀=0

x₀=Acosφ=x₀cosφ

所以(www.daowen.com)

cosφ=1

故

φ=0

则振动方程为

例7-2　一质量为0.01kg的物体做简谐运动，其振幅为0.08m，周期为4s。起始时刻物体在x=0.04m处，向Ox轴负方向运动。试求：

（1）t=1.0s时，物体所处的位置；

（2）由起始位置运动到x=0处所需要的时间。

解　（1）设简谐振动方程为

x=Acos（ωt+φ）

由题意知A=0.08m, T=4s，则有

又因t=0时，位移为x₀=0.04m，故有

v₀=-ωAsinφ＜0

则

sinφ＞0

所以应取

则振动方程为

将t=1.0s代入上式得

（2）设物体运动到x=0处所需时间t为

得

依题意知

所以

三、简谐振动的旋转矢量法

简谐振动还可以用旋转矢量的投影来表示。如图7-4所示，从坐标原点O作一矢量A，使它的模等于简谐振动的振幅A，并使A以等于角频率ω的角速度在平面上绕O点逆时针转动。t=0时，A与x轴的夹角等于简谐振动的初相位φ，这样的矢量称为旋转矢量。在任意时刻t, A与x轴的夹角为（ωt+φ），它在x轴上的投影则为

x=Acos（ωt+φ）

将此式与式（7-3）比较可知，旋转矢量A的矢端M在x轴上的投影点的运动是振幅为A、角频率为ω、初相为φ的简谐振动。在旋转矢量和简谐振动之间存在着一定的对应关系。除了上面所谈到的A、ω、φ之外，我们还可看到，矢端M沿圆周运动的速度大小等于ωA，其方向与x轴的夹角为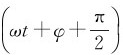，在x轴上的投影为ωAcos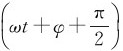=-ωAsin（ωt+φ），此即振动速度方程。矢端做圆周运动的法向加速度an=ω2A，它与x轴的夹角为（ωt+φ+π），所以加速度在x轴上的投影为

ω2Acos（ωt+φ+π）=-ω2Acos（ωt+φ）=-ω2x

正因如此，我们便可以借助于旋转矢量研究简谐振动问题，从而带来直观简便的效果。

例7-3　已知如图7-5所示的振动曲线，写出振动方程。

解　设振动方程为

x=Acos（ωt+φ）

从图中已知A=4cm，另需求出ω、φ。现利用旋转矢量法求解。

由图知t=0时，x₀=-2cm, v₀=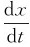＜0，旋转矢量A应在OM位置（图7-6）。

因为

所以

它与x轴的夹角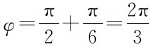，其值等于振动的初相。

当t=1s时，x₁=2cm, v₁=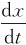＞0，则旋转矢量A应在ON位置（图7-6）。

因为

所以

A与x轴的夹角为

所以

φ′-φ=ωt=π

又知t=1s，旋转矢量的角速度为

ω=πrad/s

其值等于简谐振动的角频率。因此得振动方程为