§6-5　磁场的能量

我们已经研究过电场的能量。现在从功、能的角度来分析电路中发生的电磁感应现象，从而探讨磁场的能量。

图6-19所示的电路中，由电动势为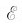的电源、自感为L的线圈和电阻R组成。当把电路接通时，电流从零起逐渐增加此时，线圈中的自感电动势阻碍电流的增长，电源就需要克服自感电动势做功，从而将电源供给的部分能量转化为另一种能量。而电流从零起的增长过程也正是其磁场的建立、加强的过程。由此可知，电源克服自感电动势所做的功就在建立磁场的过程中转化为磁场的能量。

设在电流从零增加到稳定值I的过程中，某一时刻t，线圈中的电流为i，则自感电动势为

由闭合电路的欧姆定律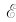+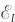=Ri，可得

上式两边同乘以idt得

设t=0时，I=0；t=t时电流增长到I，则上式积分为

式中，∫^t₀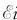idt为由0到t的时间内电源供给的能量；∫^t₀Ri²dt为在这段时间内在电阻上转化为焦耳热的能量；而LI²则为电源克服自感电动势做的功，从而转化为载流线圈的磁场的能量。所以，自感系数为L的线圈在通以电流I时，磁场的能量为

我们知道，体积为V的长直螺线管的自感系数为L=μn²V。当它通以电流I时，螺线管中的磁感应强度为B=μnI。将它们代入式（6-11），得

对于无限长的密绕载流螺线管，可视为其磁场是分布在体积为V的空间内的均匀磁场，由此可得磁场的能量密度w_m为

由于B=μH，所以上式又可写成(www.daowen.com)

或

式（6-12）虽然是由长直螺线管这一特例导出的，但是可以证明，它适用于一切磁场。

例6-10　如图6-20所示，一同轴电缆由两个长直同轴金属圆筒组成。内外圆筒半径分别为R₁和R₂，其间充有磁介质。内外圆筒上的电流大小均为I，方向相反。求：

（1）单位长度电缆所储存的磁能；

（2）单位长度电缆的自感系数。

解　（1）由安培环路定律可知，在距轴线为r＜R₁及r＞R₂处均无磁场。在两金属圆筒之间，距轴线为r处的磁场强度和磁感应强度分别为

根据式（6-12b），该处的磁场能量密度为

取半径为r，厚度为dr，单位长度的薄层圆筒为体积元，其体积为dV=2πrdr。则单位长度电缆储存的磁能为

（2）由磁能公式W_m=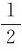LI²可求出单位长度电缆的自感系数为