§6-4　自感和互感

我们知道，引起电磁感应现象的方式是多样的。在6-2节中，将感应电动势区分成动生电动势和感生电动势；同时，又可将感应电动势区分为自感电动势和互感电动势。

一、自感

当回路中通有电流时，它所激发的磁场的磁感应线会穿过自身回路，从而给回路提供磁通量。当电流发生变化时，穿过自身回路的磁通量也将随之变化，因而在回路中产生感应电动势。这种因回路电流变化而在自身回路中引起的电磁感应现象叫做自感现象，所产生的感应电动势叫做自感电动势。

设回路中通过的电流为I，由毕—萨定律可知，它在空间任一点的磁感应强度B的大小都和电流I成正比。因此，穿过自身回路的磁通量Φ也应和电流I成正比。即

Φ=LI

比例系数L称为回路的自感系数，简称自感。它是表征回路本身性质的物理量，只与回路的大小、形状、匝数及介质的情况有关；而与其电流无关。由式（6-7a）可以看出，自感系数在数值上等于当回路中通过单位电流时，穿过自身回路所包围面积的磁通量。

当回路是由N匝线圈构成时，式（6-7a）应改写为

Ψ=NΦ=LI

式中，Ψ=NΦ是N匝线圈的磁通链。N匝线圈的自感系数在数值上等于回路中的电流为1个单位时穿过该线圈的磁通链。

根据法拉第电磁感应定律，由式（6-7a）可得回路中的自感电动势为

如果回路的形状、大小和周围磁介质的磁导率都不变，则回路的自感系数L保持不变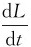，=0，于是可得

式（6-8）中的负号是楞次定律的数学表示。它指出，自感电动势将反抗回路中电流的改变。也就是说，电流增加时，自感电动势与原来电流的方向相反；电流减少时，自感电动势与原来电流的方向相同。自感电动势起着反抗回路中电流变化的作用。实际上，任何载流回路都有保持原有电流不变的特性，这种特性称为电磁惯性。

在国际单位制中，自感的单位是亨利，简称亨，用H表示。由式（6-7a）可知，

1H=1Wb/A

在工程技术与日常生活中，自感现象有广泛的应用。自感元件是构成电路的三种基本无源元件之一。由于它具有阻滞电流变化的电磁惯性，常用做交变电路中的限流元件，如在线路中常用的扼流圈、日光灯的镇流器等；在电子电路中，利用自感线圈和电容组成谐振电路和滤波器等。大型电动机的绕组线圈都有较大的自感，在断开电路时，会产生很大的自感电动势，击穿介质，形成电弧和过大的暂态电流，造成破坏作用。因此，在大功率的电力系统中，一般都加有特殊开关装置，先增加电阻使电流减小后再断开电源或加装灭弧装置。

例6-7　有一长密绕螺线管，长度为l，横截面积为S，线圈的总匝数为N，管中介质的磁导率为μ。求其自感。

解　对于长直螺线管，当有电流I通过时，可以把管内的磁场看做是均匀的，其磁感强度B的大小为

B的方向可看成是与螺线管的轴线平行的。因此，穿过螺线管每一匝线圈的磁通量都等于

而穿过螺线管的磁通链为

由NΦ=LI，得

设螺线管单位长度上线圈的匝数为n，螺线管的体积为V, V=lS，有n=N/l，故上式可写为

L=μn²V

二、互感

设有两个邻近的线圈1和2，分别通有电流I₁和I₂（图6-16）。I₁激发的磁场会产生穿过线圈2的磁通量Φ₂₁。同样，I₂的磁场也会产生穿过线圈1的磁通量Φ₁₂。当任一线圈中的电流发生变化时，都会引起另一线圈中的磁通量发生变化，而在另一线圈中激发感应电动势。这种现象称为互感现象。所产生的电动势称为互感电动势。

假设这两个线圈的形状、大小、相对位置和周围磁介质的磁导率都不改变。根据毕—萨定律，由I₁在空间任一点产生的磁感应强度都与I₁成正比，因此由I₁产生的通过线圈2的磁通量Φ₂₁也必然与I₁成正比，亦即

Φ21=M21I1(www.daowen.com)

同理，I₂产生的通过线圈1的磁通量Φ₁₂有

Φ₁₂=M₁₂I₂

式中，M₁₂和M₂₁是两个比例系数，它们只与两个线圈回路的形状、大小、相对位置以及周围磁介质的磁导率有关。可以证明，M₁₂=M₂₁=M, M称为两回路的互感系数，简称互感。这样，以上两式则可写成

Φ₂₁=MI₁，Φ₁₂=MI₁

由上式可知，两个回路的互感系数，在数值上等于其中一个回路中的电流为一个单位时，通过另一回路所包围面积的磁通量。

若两回路的形状、大小及相对位置保持不变，周围的磁介质为不变的非铁磁质，则互感系数为恒量。根据法拉第电磁感应定律，由式（6-9）可得，当线圈1中的电流I₁发生变化时，在线圈2中引起的互感电动势为

而当线圈2中的电流I₂发生变化时，在线圈1中引起的互感电动势为

式（6-10）中的负号，表明在一个线圈中所引起的互感电动势，要反抗另一个线圈中的电流的变化。

互感系数的单位和自感系数相同。实际上，二者都不易计算，一般用实验的方法测定。

互感现象在电工、电子技术中的应用非常广泛。通过互感可使能量或信号很方便地从一个回路耦合到另一个回路中去。利用互感原理制成了变压器及各种互感器等。当然，有时互感现象也会给某些电路形成不应有的干扰，也需要采取一定措施加以避免。

例6-8　无限长直导线近旁放一共面的矩形线圈，线圈长为l，宽为a，一条边离直导线为d，如图6-17所示。求长直导线与线圈的互感系数。

解　设长直导线中通有电流I，则通过矩形线圈的磁通量为

由式（6-9）得

例6-9　如图6-18所示，一长直螺线管C₁，长为l，横截面积为S，共绕有N₁匝表面绝缘的导线。在螺线管C₁上再绕另一与它共轴的线圈C₂（长亦为l），共绕N₂匝表面绝缘的导线。C₁称为原线圈，C₂称为副线圈，螺线管内均匀磁介质的磁导率为μ。求：

（1）这两个共轴螺线管的互感系数；

（2）两个螺旋管的互感系数和自感系数的关系。

解　（1）设原线圈C₁中通有电流I₁，则管内均匀磁场的磁感应强度为

磁通量为

由于磁场集中在螺线管内部，所有磁力线都通过副线圈C₂，所以通过副线圈的磁通量Φ₂₁即为上面算得的Φ。通过副线圈的磁通链Ψ₂₁为

由式（6-9）得

（2）由例6-7中对自感L的计算可知，长直螺旋管的原、副线圈的自感系数分别为

由此可得

M₂=L₁L₂

即

一般情况下，上式应写为

式中，k称为耦合系数，其值取决于两线圈的耦合程度。通常情况下k＜1，只有当两个线圈各自产生的磁场的磁感应线完全通过对方线圈（k=1，称为紧耦合）时，才有M=。