§6-2　动生电动势和感生电动势

法拉第电磁感应定律指出，只要通过回路的磁通量发生变化，回路中就会产生感应电动势。使磁通量发生变化的方式，概括起来可分为两类：一类是磁场保持不变，导体相对恒磁场运动，通过这种方式产生的感应电动势称为动生电动势；另一类是导体不动，而磁场发生变化，以这种方式产生的感应电动势称为感生电动势。

一、动生电动势

如图6-4所示，在磁感应强度为B的均匀磁场中，有一长为l的导线OP，以速度υ运动，且υ与B垂直。导线内每个自由电子也都以速度υ定向运动。因而导体内每个自由电子均受到洛伦兹力Fm的作用，并有

F_m=-eυ×B

式中，-e为电子电荷，F_m的方向与υ×B的方向相反，由P指向O。它驱使电子沿导线由P向O移动，致使O端积累了负电；P端则积累了正电，从而在导线内建立起静电场。当作用在电子上的静电场力F_e与洛伦兹力F_m相平衡（F_e+F_m=0）时，O、P两端间便有了稳定的电势差，P端电势比O端电势高。因此，这段导线相当于一个电源。它的非静电力就是洛伦兹力F_m，所以导线中非静电的电场强度E_k为

E_k的方向与υ×B的方向相同，由O指向P。由电动势的定义可得，导线OP中所产生的动生电动势为

由于υ⊥B，而且矢积（υ×B）的方向与dl的方向相同，故上式可化为

对于一段弯曲导线L在非均匀磁场中运动，而且导线上各处的运动速度也不尽相同，一般情况，可以将导线分成许多导线元dl，它可视为具有同一运动速度υ处于均匀磁场B中。由此可得线元dl中的非静电场强为

则该导线中的动生电动势为

式（6-4）就是计算动生电动势的一般公式。

二、感生电动势

在图6-3所示的电磁感应现象中，线圈A保持不移动。由于螺绕环中电流变化，使其产生的磁场发生变化，从而在线圈A中产生感应电动势和感应电流。由于线圈未移动，这时与感应电动势相应的非静电力显然不是洛伦兹力。我们知道，不论导体回路形状、性质如何，只要磁场变化使穿过回路的磁通量发生变化，就会有数值为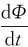的感生电动势在回路上产生。说明感生电动势的产生是变化的磁场本身引起的。麦克斯韦在分析了法拉第等人研究成果的基础上，提出了一种假说：变化的磁场在其周围空间要激发一种电场，这种电场叫做感生电场或涡旋电场。这种电场与静电场的共同之处是都对电荷有作用力。但它与静电场也有明显的不同之处：首先，静电场是由静止电荷激发，而感生电场是由变化的磁场激发；其次，静电场的电场线是始于正电荷，终于负电荷，而感生电场的电场线则是闭合的。由此可知，感生电场的环流可以不为零，它不是保守场。若用Ek表示感生电场强度，则对任意闭合回路L，按电磁感应定律则有

上式中的Φ为通过闭合回路所包围面积的磁通量。由于该磁通量为

Φ=∫_SB·dS

所以式（6-5）可以写成

若闭合回路是静止的，它所包围的面积S也不随时间变化，则上式亦可写成

这是麦克斯韦方程组的基本方程之一。

应当指出，不论空间有无导体回路或介质存在，变化的磁场均能激发感应电场。式（6-5）和（6-6）也都是普遍适用的。

例6-2　一根长为L的铜棒，在磁感强度为B的均匀磁场中以角速度ω在与磁场方向垂直的平面内绕棒的一端O匀速转动（图6-5）。求铜棒上的动生电动势。

解　在铜棒上取极小的一段线元dl，其速度为υ，并且υ、B、dl互相垂直。该线元上的动生电动势为

由于铜棒是许多长度为dl的线元组成的，且每一线元的线速度υ都与B垂直，注意到υ=lω，则可得铜棒上的电动势为

动生电动势的方向与铜棒中非静电场强度E_k=υ×B的方向相同，即由O端指向P端。(www.daowen.com)

例6-3　如图6-6所示，长为L的直导线ab，以速率υ沿平行于载流I的长直导线运动。导线ab与长直导线垂直且共面。a端至长直导线的距离为d。求导线ab上的动生电动势。

解　由于导线ab上各处的磁场大小不同，在导线ab上距长直导线为x处取线元dx，其方向由a指向b。该线元所在处磁感应强度大小为B=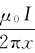，B的方向垂直纸面向外。由于B、υ与线元矢量互相垂直，则线元dx上的动生电动势为

所以，导线ab上的动生电动势为

其方向与E_k=υ×B的方向相同，即由a指向b。

例6-4　如图6-7所示，刚性弯曲导线ab以速度υ沿平行于载流I的长直导线运动。导线ab与长直导线共面，a端与b端至长直导线的垂直距离为d和d+L。求导线ab上的动生电动势。

解　建立垂直于长直导线的x坐标轴如图6-7所示。在导线ab上取线元dl，它与长直导线的距离和夹角分别为x和θ。该处的磁感应强度大小为B=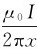，方向垂直纸面向里。υ×B的方向与dl之间的夹角为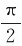+θ，dl在x方向的投影为dlsinθ=dx，则

因为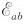＜0，所以电动势方向为由b指向a。

例6-5　如图6-8所示，半径为r的导体圆环处在磁感应强度为B的磁场中，绕垂直于B的直径以角速度ω旋动。弧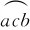对应的圆心角为45°，a在轴上。求：

（1）任一时刻t，整个圆环上的感应电动势；

（2）任一时刻t，弧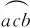上的感应电动势。

解　（1）设t=0时线圈平面法线n垂直纸面向里，即n与B的夹角φ₀=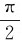，则t时刻n与B的夹角为φ=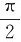+ωt，此时通过线圈平面的磁通量为

所以整个圆环上的感应电动势为

（2）在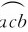上取dl如图6-8所示，则dl=rdθ，t=0时，dl的速度υ与B的夹角φ₀=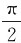；在t时刻，υ与B的夹角为φ=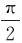+ωt。υ×B的方向与dl方向的夹角为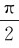-θ，所以dl上的感应电动势为

则在弧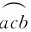上的感应电动势为

例6-6　在半径为R的无限长螺线管中，通以变化的电流，使得螺线管内部的磁场随时间线性变化，并且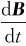=常量。求管内、外的感生电场强度Ek。

解　由于磁场分布的对称性，变化磁场所激发的感应电场的电场线，在管内外都是以管的轴线为圆心的同心圆。在同一条圆形电场线上，E_k的大小相等，其方向与圆周处处相切。任取半径为r的圆形电场线为闭合回路，如图6-9（a）所示，则

由此得到距离轴线为r处的感生电场强度Ek的大小为

当r＜R时，所考察的场点在螺线管内，选回路所包围的面积为积分面，在该面上各点变化率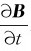相等，且和该面的法线方向平行。故有

代入式（1）可得螺线管内离轴线r处的感生电场强度Ek的值为

当r＞R时，因为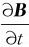只在管内存在，故有

代入式（1）可得

由以上结果可知，当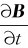＞0时，E_k的方向与积分路径的绕向方向相反。若有半径为r的导体回路，则形成与回路绕向相反方向的感应电流。若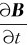＜0，则会形成与积分绕向相同方向的电流。这与楞次定律的结论是一致的。