§5-5　洛伦兹力　霍耳效应

一、洛伦兹力

导线中的电流是由带电粒子的定向运动形成的。因此，磁场对载流导线作用的安培力，实质上是磁场对载流导线中运动的带电粒子作用的宏观表现。磁场对运动电荷的作用力，称为洛伦兹力。根据安培定律可知，电流元Idl在磁感应强度为B的磁场中所受的安培力为

dF=Idl×B

考虑到电流强度I=qnSv，而电流元则可写成

Idl=qnSvdl=dNqv

式中，dN=nSdl为电流元中运动带电粒子的个数。所以，安培定律的表达式则可写成

dF=dNqυ×B

因此，每一个运动带电粒子所受的磁场力为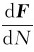，即

f=qυ×B

该式为洛伦兹力的数学表达式。它表明，洛伦兹力垂直于由υ和B所决定的平面，它既垂直于B，又垂直于带电粒子的运动方向。因此，洛伦兹力不做功。它不能改变电荷运动的快慢，而只能改变电荷的运动方向。

应该指出，尽管磁场对载流导线作用的安培力和对带电粒子的洛伦兹力本质上都是磁场对运动电荷的作用力，但是安培力和洛伦兹力是有原则区别的。磁场中载流导线内的带电粒子受到洛伦兹力后，通过载流子与组成金属导线的单晶体的晶格点阵相碰撞，将受到的洛伦兹力传递给金属导线才转变为载流导线受到的安培力。

二、带电粒子在磁场中的运动

一个质量为m，带电量为q的粒子，以速度υ进入磁感应强度为B的均匀磁场后，忽略重力，它仅在洛伦兹力的作用下运动。其运动规律有以下几种情况：

1.υ与B平行

当υ与B平行时，由式（5-21）可知，带电粒子受力为零，粒子将做匀速直线运动。

2.υ与B垂直

如图5-20所示，当υ与B垂直时，带电粒子所受的洛伦兹力大小为f=qvB=恒量，其方向与运动速度垂直。在此力的作用下，粒子将做匀速率圆周运动。由牛顿运动定律可得

所以，带电粒子做圆周运动的回旋半径为

粒子绕圆形轨道运动一周所需的时间（回旋周期）为

以上结果表明，当B、q、m给定后，R与v成正比，粒子的速率越大，其圆周轨道的半径越大，而其圆周运动的周期与速率和轨道半径无关，仅由q、m、B确定。

3.υ与B之间有任意夹角

如图5-21所示，可将υ分解为平行于B的分量v_//和垂直于B的分量v_⊥。速度的垂直分量v_⊥使带电粒子在垂直于磁场的平面内做圆周运动，速度的平行分量v_//使带电粒子沿磁场的方向做匀速直线运动。粒子同时参与这两个运动，其轨迹为螺旋线。显然，螺旋线的半径为(www.daowen.com)

回旋周期为

粒子回旋一周所前进的距离称为螺距，其值为

由上述结果可知，m、q相同的粒子在同一磁场飞行时，其回旋周期相同。如使其v_//相同，则它们的螺距也相同。带电粒子在磁场中的螺旋线运动原理，被广泛应用于磁聚焦技术上。

图5-22是磁聚焦装置示意图。从电子枪阴极K射出的电子被加速后会聚于P点，加速阳极A有一较小圆孔的共轴限制膜片，从而使得进入磁场的电子的速度υ与B的夹角都很小，故有

v_//=vcosθ≈v

v_⊥=vsinθ≈vθ

又由于在P点电子的速率v大致相同，则它们的B向分速度v_//大致相同；而v_⊥分量各不相同。它们从P点出发，v_⊥不同的各电子虽经不同半径的螺旋线前进，但通过相同的一个螺距后，将又会会聚于P′点。

三、霍耳效应

如图5-23所示，将宽为b，厚度为d，载有电流I的导电板，放在磁感应强度为B的均匀磁场中，B与电流的方向垂直且与上下板面平行。实验表明，在金属板上下两表面之间，就会检测出横向电势差UH，这种现象称为霍耳效应。电势差UH称为霍耳电势差。

实验表明，霍耳电势差UH的大小与电流I及磁感应强度B成正比，而与板的厚度d成反比，即

其中，RH是仅与导体材料有关的常数，称为霍耳系数。

霍耳效应是导体板中的载流子受到洛伦兹力作用的结果。如图5-23所示，带电荷q的载流子以速度v运动，它将受到洛伦兹力f_m=qυ×B的作用而向下移动，使导电板的上下表面分别聚积负电荷和正电荷，从而在导体内形成方向向上的电场E。在电场E的作用下，载流子又受到方向向上的电场力f_e=qE，当f_e=-f_m时，达到稳恒状态。此时有

qE=qvB

E=vB

上下两板之间的电势差大小为

U_H=Eb=vBb

由于电流的大小为I=qnSv=qnvbd，则v=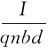，代入上式得

与式（5-28）比较可得

若图5-23中的载流子带负电荷，其漂移速度的方向与电流的方向相反。经分析可知，此时的霍耳电势差的极性与载流子带正电时的极性相反。因此，从霍耳电势差的正负极性可以判断载流子是带正电荷还是负电荷。在金属导体中，由于自由电子的数密度很大，因而金属导体的霍耳系数很小，相应的霍耳电压也就很弱。在半导体中，载流子数密度要低得多，因而半导体的霍耳系数比金属导体大得多，所以半导体能产生很强的霍耳效应。利用霍耳效应制成的霍耳元件，在生产和科研中，判别材料的导电类型、确定载流子数密度与温度的关系、测量温度、测量磁场、测量电流等得到了广泛的应用。

例5-10　设宽为0.5cm、厚为0.1mm的银质薄片中通有2A的电流，且有0.8T的磁场垂直薄片。求产生的霍耳电势差。（银的密度为10.5g/cm3）

解　银原子为单价原子，每个原子给出一个自由电子，则自由电子的数密度等于银原子的数密度n。已知银的相对原子质量为108，1mol银（0.108kg）有N₀=6.0×10²³个原子。银的密度ρ=10.5×10³kg/m³，所以

由式（5-28）可求出霍耳电势差为