§5-4　磁场对载流导线的作用

一、安培定律

磁场对载流导线的作用力称为安培力。安培通过对许多实验结果的分析，总结出了载流导线上的电流元在磁场中受力的基本定律，称为安培定律。其内容如下：

位于磁场中某点的电流元Idl，将受到磁场的作用力dF。dF的大小与电流元的电流I、长度dl、电流元所在处的磁感应强度B的大小，以及电流元和磁感应强度B的夹角的正弦成正比。其数学表达式为

dF=kBIdlsin（Idl, B）

dF的方向垂直于Idl与B所确定的平面，指向按右手螺旋法则确定，即为Idl×B的方向，如图5-15所示。上式中的比例系数k决定于式中各量的单位，在国际单位制中k=1.把上式改成矢量式为

dF=Idl×B

有限长载流导线所受的安培力等于其各个电流元所受安培力的矢量和

F=∫_LIdl×B

如果有一段长为L，通电流为I的任意形状的载流导线，放在磁感应强度为B的均匀磁场中（图5-16），由于此时在式（5-20）中的I和B均为常数，则有

式中，∫dl为该段导线上各线元的矢量和，它等于由起点a指向终点b的矢径（起点、终点根据电流流向决定），所以有

F=IL×B

显然，这与由a至b的一段载流为I的直导线所受的磁场力相同。进而，根据这一结论不难推得，闭合的通电回路在均匀磁场中所受的合力为零。

由于不能获取单独的电流元，所以无法用实验直接验证安培定律。但根据式（5-20）可以计算各种类型的电流在磁场中所受的安培力，其结果都和实验相符合，从而间接证明安培定律的正确性。

例5-7　如图5-17所示，一半径为R的半圆形闭合回路中通以电流I，回路处于磁感应强度为B的均匀磁场中，回路平面与B垂直。求磁场作用于闭合回路上的安培力。

解　整个闭合回路所受的安培力为直径上的一段直导线与半圆形电流所受安培力的矢量和。由式（5-21）可知，直径上的一段电流所受的力F₁的大小为

F₁=BI2R

F₁的方向沿负y轴方向。

在半圆形导线上任取一电流元Idl，该电流元受到的安培力dF的大小为

dF=BIdl

dF方向沿径向向外。它沿x轴和y轴的分量分别为

dF_x=-dFcosθ，dF_y=dFsinθ

由对称性分析可知

F_x=∫dF_x=0

故半圆形电流所受安培力F₂的大小为

F₂=∫dF_y=∫BIdlsinθ

由于dl=Rdθ，所以

F₂=F_y=∫^π₀BIRsinθdθ=2BIR

F₂的方向沿y轴方向，即与F₁等值反向，即F₂=-F₁，故闭合回路所受合力为

F=F₁+F₂=0(www.daowen.com)

二、均匀磁场对载流线圈的作用

如图5-18所示，在磁感应强度为B的均匀磁场中，有一刚性矩形载流线圈abcda，边长分别为l₁和l₂，载电流为I。en为线圈平面的法向单位矢量，其指向与线圈中的电流流向成右手螺旋关系。设en与磁感应强度B之间的夹角为φ，即线圈平面与B之间的夹角为θ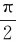（-φ）。线圈的ab和cd两边与B垂直。

根据式（5-21）可求得磁场对bc和da段的作用力分别为

F₁=BIl₂sinθ

F′₁=BIl₂sin（π-θ）=BIl₂sinθ

这两个力大小相等，方向相反，并且作用在同一直线上，它们对线圈的作用相互抵消。ab边和cd边所受的磁场作用力F₂和F′₂的大小相等，即

F₂=F′₂=BIl₁

它们的方向相反，但不在同一直线上，而形成一力偶。其对载流线圈作用的力矩大小为

M=F₂l₂sinφ=BIl₁l₂sinφ=BISsinφ

式中，S=l1l2为线圈的面积。它与线圈中电流I的乘积为载流线圈的磁矩m的大小，其方向与载流平面线圈的法线方向一致，即m=ISen，因此，上式则可写成

M=mBsinφ

由图5-18（b）可看出，力矩M的方向与e_n×B的方向一致，则磁场对载流线圈作用的力矩M可写成矢量式

M=m×B

若上述的载流线圈换成N匝，则其磁矩为m=NISe_n，该线圈所受的磁力矩为

M=m×B=（NISe_n）×B

上式虽然是从矩形平面线圈这一特例导出的，但可以证明，对于均匀磁场中的任意形状的平面载流线圈均成立。

当载流线圈处于如下几个特殊情况时，它所受力矩情况为：

（1）当φ=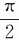时，即线圈平面与磁感应强度B平行，M=NBIS，线圈所受的力矩最大；

（2）当φ=0时，即线圈平面与B垂直，M=0，线圈所受力矩为零，此时线圈处于稳定平衡状态；

（3）当φ=π时，M=0，线圈所受力矩为零，此时线圈处于非稳定平衡状态。

由以上分析可知，磁场对载流线圈作用的磁力矩，总是使载流线圈的磁矩m转向B，直至二者方向一致，达到稳定平衡时为止。

例5-8　如图5-19所示，在Oxy平面内有半径为R，圆心在原点，通以电流I的圆形载流线圈，放在磁感应强度为B的均匀磁场中，可绕y轴转动。B的方向沿x轴方向。试证明线圈所受的磁力矩为πBIR²。

证明　在圆形载流线圈上，取电流元Idl如图5-19所示，它所受磁力的大小为

dF=BIdlsinθ=BIRsinθdθ

其方向垂直圆面向外。它对y轴的力矩大小为

dM=dFRsinθ=BIR²sin²θdθ

于是，作用在整个线圈上的磁力矩M的大小为

M=BIR²∫^2π₀sin²θdθ=πBIR²