§5-3　安培环路定理

一、安培环路定理

在第4章中我们曾导出静电场的环路定理，即电场强度E沿任意闭合路径的线积分为零。说明静电场是保守力场；而磁感应线为闭合曲线，则磁感应强度B沿任意闭合路径的积分不为零。由此说明，磁场是非保守力场。这是磁场与电场又一不同的基本性质。

我们以长直载流导线磁场的特殊情况来推导安培环路定理。在无限长直线电流的磁场中，取一平面与长直导线垂直[图5-10（a）]，在这一平面内取包围电流的任一闭合曲线L，在曲线L上任一点A的磁感应强度大小为

式中，I为长直载流导线中的电流；r为A点至导线的垂直距离。B的方向在平面上且与矢径r垂直。在闭合曲线上A点的线元dl与B的夹角为θ，如图5-10（b）所示。则

dlcosθ=rdφ

故磁感应强度B沿闭合曲线L的线积分为

所以

∮_LB·dl=μ₀I

上式中，积分回路的绕行方向与电流的流向呈右手螺旋关系。若绕行方向不变，而电流反向，则

∮_LB·dl=∮_LBdlcos（π-θ）=-μ₀I=μ₀（-I）

∮_LB·dl=μ₀I

可以认为，当电流方向与积分路径的绕行方向满足右手螺旋关系时，电流为正；反之为负。若以I表示电流的代数值，上述的两种情况可统一写为

如图5-11所示，当所取闭合回路不包围电流时，若沿闭合路径积分一周，矢径将沿相反转向再回到初始位置，即有∮dφ=0。因此有

对于在闭合回路内外存在多个电流的一般情况，可综合以上的结论来进行讨论。

设在闭合回路内有电流I₁、I₂、……I_k，在闭合回路外有电流I_k+1、I_k+2、……I_n。根据磁场的叠加原理，该回路上任一点的磁场都是所有电流共同激发的，即有

B=B₁+B₂+……+B_k+B_k+1+B_k+2+……+B_n

则

即磁感应强度B沿闭合回路L的线积分，等于闭合回路所包围的电流的代数和与真空磁导率μ0的乘积。

以上的讨论虽然是对长直载流导线而言的，但其结论具有普遍性。对于稳恒电流产生的磁场，不论电流在闭合回路内、外如何分布，都具有如上所述的共同特性。这一普遍规律性的关系式称为安培环路定理，可表述为：在真空中的稳恒电流磁场中，磁感应强度B沿任意闭合路径L的线积分（B矢量的环流），等于穿过该闭合路径所包围的电流的代数和与真空磁导率μ₀的乘积。其数学表述为

∮_LB·dl=μ₀∑I

上式中的电流I为代数值，当电流的方向与回路L的绕行方向符合右手螺旋法则时，电流I为正；反之I为负。当∮_LB·dl=0时，只说明回路L所包围的电流的代数和为零，而并非回路L上各点的B一定为零。如果I不穿过回路L，它产生的B对沿回路L的积分无贡献，而并非它在回路上各点未产生磁场。

二、安培环路定理的应用举例(www.daowen.com)

1.无限长载流圆柱体的磁场

例5-4　在横截面半径为R的无限长圆柱体中，沿轴向通有电流I，且电流在横截面上均匀分布。求圆柱体内、外的磁感应强度。

解　由于电流分布的对称性，其磁感应线为一系列以圆柱的轴线为圆心的同心圆。若取沿半径为r的圆形磁感应线为闭合路径，则在此圆周上各点的磁感应强度大小相等，方向沿圆周的切线方向（图5-12）。故可依据安培环路定理计算如下：

（1）若r＞R[图5-12（a）]，则有

∮_LB·dl=B2πr=μ₀I

由此可见，均匀载流无限长圆柱体外部的磁场分布与电流集中于圆柱轴线上的一根载流长直导线的磁场相同。

（2）若r＜R[图5-12（b）]，则有

2.载流长直螺线管内的磁场

例5-5　图5-13所示为一长度远大于横截面线度的长直螺线管。在其单位长度上均匀密绕n匝线圈，通过的电流为I。求螺线管内部的磁感应强度。

解　磁场分布如图5-13所示。在螺旋管内的中部，是磁感应线与管轴平行的均匀磁场；而在管外的中部，靠近管壁的磁感应强度近似为零。现取如图5-13所示的矩形回路ABCD为闭合路径，其中AB段、CD段与管壁平行，则磁感应强度B沿BC段、CD段、DA段的积分均为零，所以，根据安培环路定理则有

则

B=μ0nI

上式表明，无限长载流螺线管内中部，磁感应强度的大小与通过螺线管的电流和单位长度线圈的匝数成正比。

3.载流螺绕环内的磁场

例5-6　图5-14为一螺绕环，环内为真空。环上均匀地密绕有N匝线圈，线圈中的电流为I。求螺绕环内的磁感应强度。

解　由于环上的线圈绕的很密，环外的磁场可以忽略不计，磁场几乎全部集中在环内。由于电流分布的对称性使环内的磁感应线为以螺绕环中心O为圆心的同心圆，且在同一圆周上各点B的大小相等，方向沿圆周的切线方向。现取沿半径为R的圆形磁感应线为闭合路径（图5-14），则根据安培环路定理，可得

∮B·dl=B·2πR=μ₀NI

则

上式表明，螺绕环内的横截面上各点的磁感应强度是不同的。当螺绕环中心线圆周的直径2R比线圈的直径d大得多时，可以认为R为环的平均半径。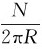=n为螺绕环的匝密度，此时式（5-17）可改写为

B=μ₀nI

管内的磁场可近似看成是均匀磁场。