§5-2　毕奥—萨伐尔定律

一、毕奥—萨伐尔定律

在静电学中，任意形状的带电体所激发的电场的电场强度E可视为许多电荷元所产生的电场强度dE的叠加。这启示我们，任意形状的载流导线在空间某点P处所产生的磁感应强度B也可以看成是导线上各个电流元Idl在该点激发的磁感应强度dB的叠加。19世纪20年代，毕奥—萨伐尔、拉普拉斯等人通过大量的实验与分析研究，总结出了电流元激发磁场的规律，称为毕奥—萨伐尔定律，概述如下：

任意电流元Idl在某点P产生的磁感应强度dB的大小与电流元的大小成正比，与电流元Idl到P点的矢径r之间的夹角θ的正弦成正比，而与P点到电流元的距离r的平方成反比。dB的方向垂直于Idl和r构成的平面，其指向为由Idl经小于π的角转向r时由右手螺旋前进的方向，如图5-5所示。其大小的数学表示式为

式中的比例系数k与磁介质和单位制的选择有关。在国际单位制中，对于真空中的磁场为k=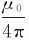，μ₀=4π×10^-7H/m，称为真空的磁导率。因此，在国际单位制中，真空中的毕奥—萨伐尔定律的表达式为

矢量式为

由叠加原理可知，任意载流导线在P点产生的磁感应强度B等于各个电流元在该点产生的磁感应强度dB的矢量和，即

由于电流元不可能单独存在，所以，毕奥—萨伐尔定律无法由实验直接验证。但是，依据该定律直接计算的载流导线在场点产生的磁场均与实验结果相符合，从而间接证实了毕奥—萨伐尔定律的正确性。

二、运动电荷的磁场

带电粒子（载流子）的定向运动形成电流。所以，电流的磁场本质上是由运动电荷激发的。下面来讨论运动电荷激发磁场的规律。

根据定义，电流I在数值上等于单位时间内通过电路截面S的电荷量。设q、n分别为载流子的电荷量和数密度，则有

式中，v为载流子的定向运动平均速度，如图5-6所示。Idl=qnSvdl=dNqv，其中dN=nSdl为该电流元中载流子的数目。由此，式（5-5b）可改写为

所以电荷量为q，速度为v的单个运动电荷激发的磁感应强度为

三、毕奥—萨伐尔定律应用举例

1.载流直导线的磁场

例5-1　求图5-7所示的载流直导线在P点产生的磁感应强度。

解　在距垂足O点为l处取电流元Idl，它在P点产生的磁感应强度dB的大小为

dB的方向垂直纸面向里。可以看出，直导线上各电流元在P点产生的磁感应强度的方向都相同。所以，载流直导线在P点的磁感应强度B的方向也垂直纸面向里，其大小为

为积分方便，可利用图中关系作如下变换：

则

dl=dcsc²θdθ

代入上式可得

式中，θ₁和θ₂分别为直导线两端的电流元与它们到P点的矢径之间的夹角；d为P点至导线的垂直距离。(www.daowen.com)

若导线的长度远大于d，则它可视为无限长的直电流，此时有θ₁=0，θ₂=π，代入式（5-7）可得

2.圆电流轴线上的磁场

例5-2　设在真空中有一半径为R，载电流为I的圆形回路（图5-8）。求其轴线上距离圆心O为x的P点的磁感应强度。

解　在圆电流上取电流元Idl，它在P点产生的磁感应强度为dB=dB_∥+dB_⊥。dB_∥与dB_⊥分别为dB在平行和垂直轴线方向的分量。显然，由于电流分布的对称性，各电流元的dB_⊥两两相互抵消，则矢量和∮dB_⊥=0，所以圆电流在P点的磁感应强度为

B=∮dB=∮dB_∥+∮dB_⊥=∮dB_∥

显然，其方向沿轴线与dB_∥同向，其大小B=B_∥，计算如下：

由于Idl与其矢径垂直，所以有

式中，r=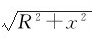，且有sinφ=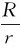，则

当x=0时，即圆心O处的磁感应强度为

3.载流直螺线管内部的磁场

例5-3　如图5-9所示，螺线管的半径为R，长度为L，匝密度为n，通有电流I。求螺线管内部轴线上P点的磁感应强度B。

解　在距P点l处取一长为dl小段，则该小段上的匝数为dN=ndl，该小段上的载流线圈等效于电流为nIdl的圆电流，它在P点产生的磁感应强度dB的大小为

由图5-9知：

l=Rcotβdl=-Rcsc²βdβ

又因

故有

将式（2）、（3）代入式（1）可得

由于各小段通电螺线管在P点产生的磁感应强度方向都相同，所以，整个载流螺线管在P点产生的磁感应强度B的大小为

式中，β₁和β₂分别为P点与螺线管两端的连线与轴线之间的夹角。

当L＞＞R时，β₁→π，β₂→0，则有

B=μ₀nI

即无限长载流直螺线管内部轴线上各点的磁场为均匀磁场。而在长直螺线管的端点处，则β₁→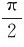，β→0，可得该处的磁感应强度为