一、磁性起源

在科学发展史上，人们对磁现象的研究比电现象早得多。我们的祖先在世界上最先认识和应用了磁现象。早在春秋战国时期，就发现了磁铁矿吸引铁的现象。11世纪北宋时，我国科学家沈括就制造出了航海用的指南针，并发现了地磁偏角。地磁的N极和S极分别在地理南极和北极附近。在磁学领域里，我国作出过巨大贡献。

在历史上很长一段时间里，人们一直认为磁和电是彼此独立、互不相关的两种现象，并分别进行研究。1820年，丹麦物理学家奥斯特发现，放在载流导线周围的磁针会受到力的作用发生偏转，如图5-1所示，从而揭示了磁现象与电现象之间的联系。同年，法国科学家安培发现，放在磁铁附近的载流导线和载流线圈也会受到作用力而发生运动。此后人们又通过实验发现载流导线和载流线圈之间也存在相互作用力。一系列的实验现象启发人们去探索磁现象的本质。1822年，安培提出了有关物质磁性本质的假说，认为一切磁现象的根源是电流。任何物质分子中都存在有圆电流，称为分子电流。分子电流相当于一个基元磁铁，物质的磁性就决定于分子电流对外界的磁效应的总和，从而说明了磁性物质的磁性也起源于电流。

安培的分子电流假说符合现代对物质磁性的解释。由于物质是由分子、原子组成的，原子是由带正电的原子核和绕核运动的电子所组成的，原子、分子内的这种运动形成等效的环形电流。电子和核还有自旋与其相联系的磁性。原子、分子以及质子、中子等微观粒子运动就构成了等效的分子电流。

通过奥斯特、安培、毕奥—萨伐尔、拉普拉斯等人的实验与理论研究，人们认识到一切磁现象都起源于电荷的运动，并逐步建立起运动电荷与电流、磁铁与磁铁以及电流与磁铁之间相互关系的经典电磁理论。

二、磁场磁感应强度

现代物理学认为，运动电荷在其周围激发一种特殊物质，称为磁场。运动电荷或电流之间、磁铁之间以及电流与磁铁之间的相互作用都是通过磁场传递的。我们可以把这种关系形象地表示为

磁场和电场一样，是客观存在的特殊形态的物质。磁场对处于其中的运动电荷或载流导体产生作用力；并且，载流导体在磁场中移动时，磁场力对载流导体做功，表明磁场具有能量。

在静电学中，我们曾引入电场强度E来描述电场，类似的，我们引入磁感应强度B来定量地描述磁场。

取一平面载流线圈，其线度必须足够小，以至于当线圈处于任何磁场中时，在线圈范围内的磁场性质均可视为处处相同。同时，线圈中的电流也足够小，将它引入磁场中时，它对原有磁场的影响可以忽略不计。这样的平面载流线圈称为试验线圈。

设试验线圈的面积为ΔS，通过线圈的电流为I₀，则定义试验线圈的磁矩为

m=I₀ΔSe_n

式中，e_n为载流线圈平面法线方向的单位矢量。法线的正方向按右手螺旋法则确定，如图5-2所示。线圈的磁矩m是矢量，是表征载流线圈本身特性的物理量。

实验发现，当把试验线圈放置在磁场中某一位置时，它将受到磁力矩的作用，只有当它转到某一方位时，磁力矩才为零，此时线圈处于平衡位置。当试验线圈处于稳定平衡位置时的法线方向被规定为该点的磁场方向。图5-2中实验所示的位置就是线圈的稳定平衡位置。当线圈从稳定平衡位置转过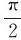时（图5-2中虚线所示位置），线圈所受磁力矩量值最大，用表示。实验指出，在磁场中任一点均有

实验表明，比值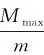仅与试验线圈的所在位置有关。在磁场中任一定点，它都有唯一定值。由此可见，比值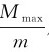反映了各点磁场的性质，我们把它定义为磁感应强度B的大小，即

综上所述，磁场中某一点的磁感应强度B是一矢量，其量值等于具有单位磁矩的试验线圈在该点所受到的最大磁力矩，其方向与试验线圈在稳定平衡位置时的法线的正方向一致。

在国际单位制中，磁感应强度B的单位是特斯拉，用符号T表示。1T=1N/（A·m）。有时也用高斯（Gs）作为B的单位，其换算关系为(www.daowen.com)

1T=10⁴Gs

三、磁通量磁场中的高斯定理

1.磁感应线

在静电学中用电场线来形象地描述电场分布；类似地，也可以用磁感应线（磁力线）来形象地描述磁场的分布。为此，我们规定：磁感应线上任意一点的切线方向与该点磁感应强度B的方向一致；在磁场中某点处，与磁感应强度B的方向垂直的面元中磁感应线的密度等于该点磁感应强度B的大小。

图5-3所示为几种典型电流磁场的磁感应线。图示表明，磁感应线具有如下特征：

（1）磁场中每条磁感应线都是环绕电流的闭合曲线，因此磁场是涡旋场。

（2）任何两条磁感应线不相交，这是因为磁场中任一点的磁感应强度B的方向是唯一确定的。

（3）磁感应线的环绕方向与电流的方向之间的关系可用右手定则表示。如图5-3（a）所示的情况，右手握住直电流，让伸开的拇指指向电流方向，则其他四指与磁感应线的环绕方向相同；而对图5-3（b）、（c）所示的情况，沿电流方向握右手，四指方向指向电流方向，则伸开的拇指指向为环管内部磁感应线的方向。

2.磁通量

通过磁场中某一曲面的磁感应线的条数，叫做通过此曲面的磁通量，用符号Φ_m表示，它的计算与电场强度通量的计算类似。如图5-4（a）所示，依据磁感应线的规定，计算曲面S上的磁通量，在S上取面元dS，则穿过面积元dS的磁通量为

dΦ_m=BdScosθ=B·dS

所以，穿过任意曲面S的磁通量为

在国际单位制中，磁通量的单位为韦伯，用符号Wb表示。

3.磁场的高斯定理

如果在磁场中任取闭合曲面S[图5-4（b）]，并规定由内向外的方向为法线正方向，则穿出闭合曲面的磁通量为正，穿入闭合曲面的磁通量为负。由于磁感应线均为无头无尾的闭合曲线，所以对闭合曲面来说，穿入的磁感应线数必然等于穿出的磁感应线数，因此，通过任意闭合曲面的磁通量恒等于零，如图5-4（b）所示。表达式为

式（5-4）称为磁场的高斯定理，它是表征磁场性质的重要定理之一，从而表明磁场是无源场。