§4-6　静电场的能量

一、电容器的能量

电容器的充电过程，实际上是充电电源克服静电场力做功，把正电荷不断地从带负电的极板搬运到带正电的极板的过程。通过电源内非静电力做功，将其他形式的能量转换为静电能储存在电容器中。设电容器的电容为C，在充电过程中的某一瞬时，极板上所带电荷量为q，两极板间电势差为u，再继续将电荷量dq从负极板移到正极板上，则电源做的元功为

若电容器C充电，使极板上的电荷量从零增至Q时，电源所做的功为

根据功能转换关系，电容器所储存的静电能We等于充电过程中电源所做的功，即有

其中，用到了电容的定义C=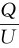。上式说明，对同一个电容器，当充电电压高或储存的电荷多时，它所储存的能量多；对不同的电容器，当充电电压一定时，电容量大的电容器储存的能量多。从这一意义上说，电容C也是电容器储能本领的标志。

二、静电场的能量

由上述讨论我们知道，电容器充电的过程是电源内非静电力做功，使电容器两极板上带等量异号电荷的过程；也是在它的两极板间建立电场的过程。电源做功使电容器极板上带电荷Q，因此电容器是储存电荷的元件；由于电源内非电静电力做功，使其他形式的能量转换为静电能，所以电容器是储能器件。大量实验证明，电容器中的能量是储存在它的两极板间的静电场中，即电场是能量的携带者。电场具有能量是电场的基本性质之一。

我们以平板电容器为例，讨论静电场中的能量。平板电容器极板间是均匀电场，因此，其能量分布也应是均匀的。电容器储存的能量W_e均匀分布在体积为V=Sd的空间中（S、d分别为极板面积和两板间距离）。考虑到平板电容器电容C=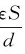，极间电压U=Ed，故有

引入电场的能量密度

为单位体积内的电能，则有(www.daowen.com)

应强调指出，上述结果虽然是从均匀电场导出的，但可以证明它是一个普遍适用的公式。对于非均匀电场，在所取的体积元dV内，电场可视为均匀的，w_e可视为常量，dV内的电场能量为dW_e=w_edV，则整个电场的能量为

例4-12　一球形电容器，内、外球壳的半径分别为R₁和R₂，如图4-29所示。两球壳间充满相对介电常数（亦称相对电容率）为ε_r的电介质。求电容器极板上带有电荷量Q时，球形电容器电场所储存的电能。

解　由于电容器内外球壳分别带电，根据高斯定理可求得两球壳间的电场强度为

取半径为r，厚度为dr的球壳为体积元dV, dV=4πr²dr。该体积元所在处电场的能量密度为

此体积元内的电场能量为

电容器中电场的总能量为

我们知道电容器储存的能量为

由此可得该电容器的电容为

这也是利用能量公式求电容器电容的一种方法。